Polinomi

Polinom stopnje n (n ∈

₀) je vsaka funkcija, ki jo lahko zapišemo z enačbo oblike:
p(x) = a_n xⁿ + a_n−1 xⁿ⁻¹ + · · · + a₂ x² + a₁ x + a₀
Pri tem so koeficienti a_n, a_n−1, . . . , a₂, a₁ in a₀ poljubna realna števila, koeficient a_n pa mora biti različen od 0 (polinom je stopnje n samo, če potenca xⁿ v polinomu res nastopa).

Koeficient a_n (koeficient pri najvišji potenci, ki v polinomu nastopa) se imenuje vodilni koeficient polinoma. Člen a_n xⁿ se imenuje vodilni člen polinoma.
Koeficient a₀ (koeficient brez x), se imenuje prosti koeficient ali tudi prosti člen polinoma.

Stopnjo polinoma p označimo: st(p)

Polinom druge stopnje je kvadratna funkcija.
Polinom prve stopnje je linearna funkcija.
Polinom ničte stopnje je konstantni polinom p(x) = a (za a ≠ 0).
Kot poseben primer uvrstimo v množico polinomov tudi ničelni polinom - to je polinom, ki je konstantno enak 0. Ničelni polinom nima definirane stopnje (pravimo tudi, da ima stopnjo minus neskončno).

Računanje s polinomi

Če v enačbo polinoma vstavimo dano število a, lahko izračunamo vrednost polinoma p(a) (vrednost polinoma v točki a oziroma vrednost polinoma pri x = a).
Polinome lahko seštevamo, odštevamo in množimo (glej računanje s funkcijami). Rezultat vsake od teh računskih operacij je spet polinom.

V množici polinomov lahko izvajamo tudi računsko operacijo deljenje z ostankom (primerjaj: deljenje z ostankom v množici naravnih števil).
Velja:
Osnovni izrek o deljenju polinomov:
Poljuben polinom deljenec p lahko delimo s poljubnim neničelnim polinomom deliteljem q in pri tem dobimo polinom količnik k(x) in polinom ostanek o(x), tako da velja
p(x) = q(x) k(x) + o(x) (tj. velja preizkus pri deljenju) in
st(o) < st(q) (tj. stopnja ostanka je manjša od stopnje delitelja)

Pri deljenju polinoma p s polinomom (x − a) je ostanek vedno število (ker je stopnja delitelja 1, mora biti stopnja ostanka manjša od 1). Izkaže se, da je to število enako vrednosti polinoma p(a).
Deljenje polinoma p s polinomom (x − a) lahko zapišemo na krajši način s Hornerjevim algoritmom.

Ničle polinoma

Če je število a ničla polinoma p, je ostanek pri deljenju polinoma p s polinomom (x − a) enak 0 (deljenje se izide brez ostanka). Torej lahko v tem primeru polinom p zapišemo v obliki:
p(x) = (x − a) k(x)

Odgovor na vprašanje, kateri polinomi sploh imajo ničle, podaja Gaußov izrek, ki ga imenujemo tudi
Osnovni izrek algebre polinomov:
Vsak nekonstanten polinom ima v

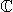vsaj eno ničlo.

Posledica Gaußovega izreka:
Polinom stopnje n (za n > 0) lahko zapišemo v razcepljeni (ničelni) obliki:
p(x) = C (x − x₁)(x − x₂) · · · (x − x_n)

Števila x₁, x₂, ..., x_n, ki nastopajo v razcepljeni obliki, so ravno vse ničle polinoma p.
Če so vsa ta števila med seboj različna, vidimo, da ima polinom stopnje n točno n ničel. Če so nekatera (ali tudi vsa) od teh števil med sabo enaka, je ničel seveda manj kot n.
Če ničla x_m v razcepljeni obliki nastopa k-krat, pravimo, da je to k-kratna ničla polinoma (oziroma ničla stopnje k). Če vsako ničlo polinoma štejemo tolikokrat, kolikor je njena stopnja, lahko rečemo, da ima polinom stopnje n vedno točno n ničel.

Čeprav so koeficienti polinoma realna (ali kar cela) števila, so ničle polinoma v splošnem lahko nerealne.
Velja pa pravilo: Če ima polinom z realnimi koeficienti nerealne ničle, potem te nastopajo v konjugiranih parih.

Iskanje ničel polinoma
Žal ne obstaja preprosto splošno pravilo za iskanje ničel polinoma.
Pri iskanju ničel najpogosteje uporabljamo naslednje metode (oziroma kombinacijo naslednjih metod):

Razcepljanje: Polinom razcepimo po pravilih za razcepljanje izrazov in iz razcepljene oblike razberemo ničle.
Inteligentno ugibanje: Ničlo a »uganemo« in s Hornerjevim algoritmom preverimo, da je to res ničla, potem pa polinom razcepimo v obliko: p(x) = (x − a) k(x).

Da je ugibanje res inteligentno, se ravnamo po naslednjih pravilih:
(1) Cele ničle polinoma s celimi koeficienti iščemo samo med delitelji prostega člena.
(2) Racionalne ničle polinoma s celimi koeficienti iščemo samo med ulomki, ki imajo v števcu delitelj prostega člena, v imenovalcu pa delitelj vodilnega koeficienta.
Numerične metode: Če druge metode odpovejo, poiščemo približne vrednosti ničel z numeričnimi metodami.
Najbolj znana numerična metoda je metoda bisekcije:

Najprej poiščemo interval [a, b], na katerem polinom (oziroma poljubna zvezna funkcija) spremeni predznak (v enem krajišču je funkcija pozitivna, v drugem pa negativna).
Potem izračunamo razpolovišče intervala: c =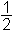 (a + b).

Ugotovimo, na katerem od manjših intervalov [a, c] ali [c, b] funkcija spremeni predznak, in postopek nadaljujemo na tem intervalu.

Če želiš izvedeti več o tem, glej dodatek: Numerične metode za reševanje enačb.

Graf polinoma

Polinom je zvezna funkcija. To pomeni, da je graf polinoma nepretrgana krivulja. Pri risanju grafa polinoma upoštevamo naslednja pravila:

Graf polinoma, ko gre x proti ±, je podoben grafu vodilnega člena tega polinoma (y = a_nxⁿ). Torej je podoben grafu potenčne funkcije y = xⁿ raztegnjene z raztegom v smeri osi y za a_n.
Graf polinoma v okolici ničle k-te stopnje je podoben kot graf potenčne funkcije y = x^k (z ustreznim raztegom in premikom).

To pomeni, da ločimo tri vrste ničel:
(1) enostavne ničle (ničle prve stopnje): graf seka abscisno os pod določenim kotom.


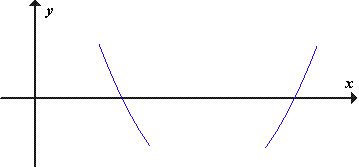
(2) ničle sode stopnje (tj. stopnje 2., 4., 6. itd): graf ne prečka abscisne osi, v ničli sode stopnje ima polinom lokalni ekstrem.


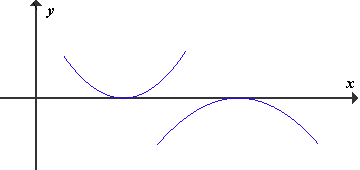
(3) ničle lihe stopnje večje od 1 (tj. stopnje 3., 5., 7., itd): graf prečka abscisno os, vendar tako, da se ji v okolici ničle zelo lepo prilega (ima vodoravno os za tangento) - pravimo, da ima graf v taki ničli vodoravni prevoj.


Torej ugotovimo: Predznak polinoma se spremeni samo v ničlah lihe stopnje.

Zgled:
Polinom p(x) = (x + 1)x²(x − 2)³ ima enojno ničlo pri −1, dvojno ničlo pri 0 in trojno ničlo pri 2.

Graf polinoma - zgled