Linearna funkcija

Linearna funkcija je funkcija, ki jo lahko zapišemo z enačbo oblike f (x) = kx + n, kjer sta koeficienta k in n poljubni realni števili.

Graf linearne funkcije

Graf linearne funkcije je premica. Ker dve točki natančno določata premico, lahko graf linearne funkcije narišemo tako, da izračunamo koordinate dveh točk.

Pogosto si pri risanju pomagamo kar s točkama, ki ju določata koeficienta k in n:
Število n pomeni presečišče grafa z ordinatno osjo (f (0) = n). Imenujemo ga odsek na osi y, ali tudi začetna vrednost (s točko N(0, n) začnemo risati graf linearne funkcije).
Število k določa smer premice, zato ga imenujemo smerni koeficient. Ustrezno točko dobimo tako, da se iz točke N pomaknemo za eno enoto v desno in za k enot navzgor (oziroma navzdol, če je k negativen).

Zgled:
Narišimo graf funkcije f (x) = 2x + 1

Risanje linearne funkcije

Če je k > 0, linearna funkcija narašča.
Če je k < 0, linearna funkcija pada.
Če je k = 0, je linearna funkcija konstantna. Graf je v tem primeru vzporeden abscisni osi. (Torej: Graf konstantne funkcije je vodoravna premica.)

Pomen k

Enačba premice

Graf linearne funkcije je premica, torej lahko enačbo premice zapišemo kot enačbo grafa linearne funkcije: y = kx + n. To obliko enačbe imenujemo eksplicitna oblika enačbe premice.
Žal v tej obliki ne moremo zapisati enačbe vsake premice v ravnini. Navpična premica (premica vzporedna ordinatni osi) namreč ni graf nobene funkcije. Enačbo navpične premice lahko zapišemo v obliki: x = m.

Če želimo vse premice v ravnini zapisati z enačbo enake oblike, moramo uporabiti implicitno obliko enačbe premice: ax + by + c = 0. Implicitna oblika enačbe premice ni enolično določena. Če enačbo pomnožimo ali delimo s poljubnim od 0 različnim številom, dobimo drugo implicitno enačbo za isto premico.
Implicitna oblika enačbe žal tudi nič ne pomaga pri risanju premice.

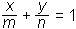
Za lažje risanje uporabljamo tudi segmentno (odsekovno) obliko enačbe premice: x/m+y/n=1

Števili m in n pomenita odseka (segmenta), ki ju premica omejuje na abscisni oziroma na ordinatni osi.
Odseka na oseh

V segmentni obliki lahko zapišemo enačbo vsake premice v ravnini, razen:
(1) navpične premice,
(2) vodoravne premice,
(3) premice, ki poteka skozi izhodišče koordinatnega sistema.

Enačba premice skozi dve dani točki

Če poznamo koordinati točk A(x₁, y₁) in B(x₂, y₂), lahko izračunamo smerni količnik premice, ki poteka skozi ti dve točki, po formuli: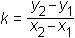
Formula za k

Število n lahko določimo s pomočjo enačbe y = kx + n (v enačbo vstavimo že izračunani k in koordinati ene od podanih točk).

Če je x₁ = x₂, je premica vzporedna ordinatni osi. V tem primeru k ne obstaja (in tudi eksplicitna oblika enačbe ne obstaja), enačbo premice pa lahko zapišemo v obliki x = m (pri tem je seveda m = x₁ = x₂).

Kot med premicama

Naklonski kot premice je kot, ki ga oklepata ta premica in abscisna os.
Za naklonski kot premice s smernim koeficientom k velja formula:
tg α = k

Če je k > 0, je α ostri kot.
Če je k < 0, lahko izberemo α na dva načina: ali izberemo topi kot ali pa negativni ostri kot.
Če je k = 0, je premica vzporedna abscisni osi. V tem primeru določimo, da je α = 0.

Kot med premicama izračunamo s pomočjo naklonskih kotov obeh premic (φ = |α₂ − α₁| ), lahko pa tudi s pomočjo smernih koeficientov po naslednji formuli:

Premici p in q sta pravokotni samo, če je imenovalec v zgornjem ulomku enak 0.
Torej velja:
p ⊥ q ⇔

(pogoj pravokotnosti)

Če sta premici p in q vzporedni, pravimo, da je kot med njima enak 0.
Velja:
p || q ⇔ k₂ = k₁ (pogoj vzporednosti)

Linearna enačba z eno neznanko

Linearna enačba (z eno neznanko) je vsaka enačba, ki jo lahko zapišemo v obliki kx + n = 0 (kjer sta koeficienta k in n poljubni realni števili).

Če je k = n = 0, potem je rešitev linearne enačbe vsako realno število: R = .
Če je k = 0 in n ≠ 0, potem je linearna enačba nerešljiva: R = { }.
Če sta števili k in n obe različni od 0, potem ima linearna enačba točno eno rešitev: R = .

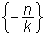Sistem dveh linearnih enačb z dvema neznankama

Sistem dveh linearnih enačb z dvema neznankama (na kratko: sistem 2 × 2) je sistem oblike:
ax + by = c
dx + ey = f
(kjer so a, b, c, d, e in f dana realna števila).

Enačbi, ki sestavljata sistem 2 × 2, sta enačbi premic v ravnini. Rešitev sistema 2 × 2 je par števil (x, y), ki geometrijsko pomeni koordinati presečišča teh dveh premic.
Sistem 2 × 2 ima lahko 0, 1 ali neskončno mnogo rešitev:

Če sta premici vzporedni, se ne sekata. V tem primeru je sistem enačb nerešljiv.
Če se premici sekata, je rešitev točno ena točka oziroma točno en par števil (x, y), namreč presečišče.
Lahko se zgodi tudi, da obe enačbi predstavljata isto premico. V tem primeru je rešitev sistema enačb vsaka točka, ki leži na tej premici.

Linearne neenačbe

Linearna neenačba z eno neznanko je vsaka neenačba, ki jo lahko zapišemo v obliki kx + n > 0 (kjer sta koeficienta k in n poljubni realni števili).
Namesto znaka > lahko nastopa tudi katerikoli od ostalih znakov neenakosti: <, ≤ ali ≥.

Linearno neenačbo z eno neznanko rešimo s preoblikovanjem po splošnih pravilih za reševanje neenačb. Rešitve ponavadi sestavljajo neskončni interval, lahko pa se zgodi tudi, da je neenačba nerešljiva ali da je rešitev vsako realno število.

Linearna neenačba z dvema neznankama je vsaka neenačba, ki jo lahko zapišemo v obliki ax + by + c > 0 (kjer so koeficienti a, b in c poljubna realna števila in a in b nista oba hkrati enaka 0).
Namesto znaka > lahko nastopa tudi katerikoli od ostalih znakov neenakosti: <, ≤ ali ≥.

Rešitve neenačbe z dvema neznankama ponavadi ponazorimo s točkami v ravnini. Množica vseh rešitev linearne neenačbe z dvema neznankama je polravnina, ki ima za rob premico z enačbo ax + by + c = 0.

Zgled:
Rešimo neenačbo: 2x − y − 1 > 0
Najprej jo preoblikujmo v lepšo obliko:
  −y > −2x + 1    / ·(−1)
   y < 2x − 1
V koordinatnem sistemu narišemo premico y = 2x − 1. Narišemo jo črtkasto, ker točke na tej premici niso rešitve (v neenačbi ne velja enačaj). Množica vseh rešitev je polravnina pod to premico (znak <).

Kazalo poglavij

Risanje grafov funkcij

Potenčna funkcija

Abecedno kazalo