Enačbe in sistemi enačb

Enačba je zapis sestavljen iz dveh matematičnih izrazov, ki ju imenujemo leva in desna stran enačbe, in iz enačaja, ki stoji med njima. V enačbi nastopajo tudi spremenljivke, ki jih v tem primeru imenujemo neznanke. Najpogosteje v matematiki srečamo enačbe z eno neznanko, ki je ponavadi označena s črko x.

Rešitev enačbe z eno neznanko je število, pri katerem je vrednost leve strani enačbe enaka kot vrednost desne strani. (Torej: če vstavimo to število namesto neznanke, dobimo na levi in desni enak rezultat.)
Če enačba vsebuje n neznank, je rešitev enačbe vsaka n-terica števil, pri kateri je vrednost leve strani enačbe enaka kot vrednost desne strani.
Vse rešitve enačbe sestavljajo množico rešitev enačbe. Množico vseh rešitev dane enačbe označimo z oznako R .

Zgledi:
(1) Enačba 2x = 6 ima samo eno rešitev in to je x = 3.
Torej je R = {3}.

(2) Enačba x + 1 = x nima rešitve, saj x + 1 nikakor ne more biti enak x.
Torej je R = { }.

(3) Enačba |x| = x ima za rešitev vsako nenegativno realno število,
torej R =

₀⁺= [0,

).

Dve enačbi sta enakovredni (ekvivalentni), če imata enaki množici rešitev.

Zgled: Enačbi 5x = 15 in 2x = x + 3 sta enakovredni, saj je za obe enačbi edina rešitev x = 3 (torej je za obe množica rešitev enaka R = {3} ).

Reševanje enačb

Enačbo rešimo tako, da jo preoblikujemo v drugo enačbo, ki je prvotni enakovredna (tj. ima isto množico rešitev), vendar pa je po obliki preprostejša.

Pri reševanju enačb uporabljamo zlasti naslednja dva postopka preoblikovanja (rezultat je vedno enačba, ki je prvotni ekvivalentna):

Levi in desni strani enačbe lahko prištejemo isto število (ali tudi neznanko ali daljši matematični izraz).
Levo in desno stran enačbe lahko pomnožimo ali delimo z istim od 0 različnim številom.

Pri reševanju enačb upoštevamo tudi naslednja opozorila:

Če levo in desno stran enačbe delimo z izrazom, ki vsebuje neznanko, dobljena enačba praviloma ni enaka prvotni, pač pa ima manj rešitev. S takim postopkom reševanja bi torej lahko izgubili eno ali več rešitev, zato praviloma enačbe ne delimo z neznanko oziroma z izrazom, ki vsebuje neznanko.
Če levo in desno stran enačbe pomnožimo z izrazom, ki vsebuje neznanko, dobljena enačba praviloma ni enaka prvotni, pač pa ima več rešitev. Takemu množenju se torej praviloma izogibamo.
Včasih pa drugačen postopek reševanja sploh ni možen. Takrat enačbo pomnožimo z izrazom, vendar pa se zavedamo, da rešitve končne enačbe niso nujno tudi rešitve prvotne enačbe. Zato je v takih primerih obvezen preizkus, s katerim preverimo, katere od dobljenih rešitev so res rešitve prvotne enačbe.
Zgled:
Spodnjo enačbo rešimo tako, da jo pomnožimo z (x − 2):

Dobimo dve rešitvi x₁ = 2 in x₂ = −2, vendar pa prva od njiju ni rešitev prvotne enačbe (izločimo jo s preizkusom). Dana enačba ima torej smo eno rešitev: x = −2.
Enačbo pogosto preoblikujemo tudi tako, da na levi in desni strani uporabimo isto funkcijo (npr. obe strani kubiramo, korenimo, logaritmiramo, ipd). Pri tem se moramo zavedati, da je dobljena enačba enakovredna prvotni, samo če je uporabljena funkcija bijektivna. Sicer pa je treba upoštevati posebne lastnosti dane funkcije (glej posamezne funkcije).

Preproste enačbe

Nekaj nasvetov za reševanje preprostejših tipov enačb z eno neznanko:

Enačbo prve stopnje (linearno enačbo) rešimo tako, da prenesemo člene z neznanko na eno stran, člene brez neznanke pa na drugo stran.

Zgled:
  3x − 5 = x + 7
  3x − x = 7 + 5
  2x = 12    / : 2
  x = 6
Enačbo višje stopnje (kvadratno, polinomsko enačbo, ipd.) rešimo tako, da prenesemo vse člene na isto stran enačbe in dobljeni izraz razcepimo. Rešitve izračunamo po pravilu, da je produkt enak 0, samo če je vsaj en od faktorjev enak 0.

Zgled:
  x² = x + 2
  x² − x − 2 = 0
  (x −2)(x +1) = 0
  x₁ = 2, x₂ = −1
Iz enačbe oblike f(x) = a izrazimo x tako, da uporabimo na drugi strani enačbe inverzno funkcijo .
Tako dobimo enačbo x = f⁻¹(a). Ta metoda je uporabna samo, če je funkcija f bijektivna.

Zgled (kubiranje v spodnji enačbi odpravimo tako, da na drugi strani enačbe uporabimo kubični koren):

Kadar zgoraj opisani običajni postopki ne pripeljejo do rešitve, lahko uporabimo numerične metode za reševanje enačb.

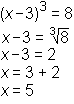
Sistemi enačb

Sistem enačb je sestavljen iz dveh ali več enačb. Ponavadi te enačbe vsebujejo tudi dve ali več neznank. Rešitev sistema enačb n-terica števil, pri kateri je v vsaki od enačb vrednost leve strani enaka kot vrednost desne strani.

Pri reševanju sistema enačb je naše glavno vodilo zmanjšanje števila enačb in neznank. Npr.: Sistem n enačb z n neznankami poskušamo preoblikovati v sistem, ki ima n−1 enačbo in n−1 neznanko.

Število neznank lahko zmanjšamo, če iz ene enačbe izrazimo eno od neznank in dobljeni izraz vstavimo v vse druge enačbe.

Zgled: Rešiti želimo sistem enačb:
   x² + y² = 25
   2x − y = 5
Iz spodnje enačbe izrazimo y = 2x − 5 in to vstavimo v zgornjo enačbo:
   x² + (2x − 5)² = 25
   x² + 4x² − 20x + 25 = 25
   5x² − 20x = 0
   5x(x − 4) = 0
  x₁ = 0   x₂ = 4
Po zvezi y = 2x − 5 (ki smo jo izpeljali zgoraj) izračunamo še ustrezni vrednosti za y in dobimo obe rešitvi sistema.
Prva rešitev je par števil: x₁ = 0,   y₁ = −5
druga rešitev je par števil: x₂ = 4,   y₂ = 3