| Kazalo poglavij | Dodatek 1 | Kazalo simbolov | Abecedno kazalo |
Numerične metode za reševanje enačb
Enačbo običajno rešujemo tako, da jo preoblikujemo v preprostejšo obliko, ki pa je prvotni enačbi enakovredna (enakovrednost pomeni, da ima nova enačba enake rešitve kot prvotna enačba). S preoblikovanjem nadaljujemo toliko časa, da dobimo točne vrednosti rešitev. Vse postopke take vrste imenujemo analitične metode za reševanje enačb.Zdaj si bomo ogledali še drugo vrsto postopkov – to so numerične metode za reševanje enačb. Bistvo numeričnih metod je računanje s približki in tudi na koncu bomo dobili le približne vrednosti rešitev. Ravno zato numerične metode uporabljamo zlasti takrat, kadar ne moremo izračunati točnih vrednosti rešitev.
Poznamo več različnih numeričnih metod za reševanje enačb v množici realnih števil. V nadaljevanju si bomo ogledali najbolj uporabne med njimi.
Metoda bisekcije
Metodo bisekcije uporabljamo za iskanje ničel funkcije oziroma za reševanje enačbe oblike f (x) = 0.Če želimo rešiti enačbo drugačne oblike, lahko vse člene prenesemo na levo stran in dobimo obliko f (x) = 0.
V enačbi torej na levi strani nastopa neka funkcije f, na desni strani pa nastopa število 0. Za zvezno funkcijo f velja naslednji premislek:
Če je zvezna funkcija f v točki a negativna, v točki b pa pozitivna (ali obratno), potem lahko sklepamo, da mora biti v neki vmesni točki vrednost funkcije enaka 0. Funkcija f ima torej na intervalu [a, b] vsaj eno ničlo.
Zdaj lahko izračunamo aritmetično sredino števil a in b: c =
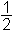(a + b).Število c razdeli interval [a, b] na dva enako velika podintervala [a, c] in [c, b]. Če izračunamo vrednost funkcije v točki c, lahko takoj vidimo na katerem od podintervalov mora biti ničla:
Ničla vedno leži na tistem podintervalu, na katerem funkcija spremeni predznak. Na tem podintervalu potem ponovimo isti postopek (interval razpolovimo in pogledamo, na katerem od manjših intervalov leži ničla).
Razpolavljanje intervala lahko ponovimo še poljubno mnogokrat. Če se po nekaj korakih slučajno zgodi, da dobimo f (x) = 0, potem smo dobili točno vrednost ničle. Sicer pa krajišči intervala predstavljata približka za ničlo.
Ime metode izvira iz latinske besede bisectio, ki pomeni razpolavljanje.
Zgled:
Rešimo enačbo:
x3 + 2x = 9
Enačbo najprej preoblikujemo v obliko:
x3 + 2x − 9 = 0
To pomeni, da iščemo ničle funkcije:
f (x) = x3 + 2x − 9
Najprej moramo poiskati interval [a, b], na katerem funkcija spremeni predznak. Z malo poskušanja ugotovimo, da to velja za interval [1, 2], saj je f (1) = −6 in f (2) = 3.
Torej bomo izbrali a = 1 in b = 2.
Zdaj začnemo s postopkom razpolavljanja. Najbolj pregledno je če celoten postopek pišemo v obliki tabele. V prva dva stolpca zapišemo krajišči intervala a in b, v tretji stolpec zapišemo razpolovišče c = (a + b)/2, v četrti stolpec pa zapišemo vrednost funkcije f (c).
| a | b | c | f (c) |
| 1 | 2 | 1.5 | −2.625 |
-
V našem primeru je f (a) negativno število.
Če je tudi vrednost f (c) negativna, potem mora ničla ležati
na intervalu [c, b], zato se odločimo, da število c
v naslednji vrstici zapišemo v stolpec a (vrednost v stolpcu b pa
samo prepišemo).
-
V našem primeru je f (b) pozitivno število.
Če je tudi vrednost f (c) pozitivna, potem pa mora ničla ležati
na intervalu [a, c], zato se odločimo, da število c
v naslednji vrstici zapišemo v stolpec b (vrednost v stolpcu a pa
samo prepišemo).
| a | b | c | f (c) |
| 1 | 2 | 1.5 | −2.625 |
| 1.5 | 2 |
Postopek potem nadaljujemo:
| a | b | c | f (c) |
| 1 | 2 | 1.5 | −2.625 |
| 1.5 | 2 | 1.75 | −0.140625 |
| 1.75 | 2 | 1.875 | +1.34179687 |
| 1.75 | 1.875 | 1.8125 | +0.57934570 |
| 1.75 | 1.8125 | 1.78125 | +0.21414185 |
| 1.75 | 1.78125 | 1.765625 | +0.03546524 |
| 1.75 | 1.765625 | 1.7578125 | −0.05290175 |
| 1.7578125 | 1.765625 | 1.76171875 | −0.00879890 |
| 1.76171875 | 1.765625 | 1.76367187 | +0.01331299 |
| 1.76171875 | 1.76367187 | 1.76269531 | +0.00225200 |
| 1.76171875 | 1.76269531 | 1.76220703 | −0.00327471 |
| 1.76220703 | 1.76269531 | 1.76245117 | −0.00051167 |
| 1.76245117 | 1.76269531 | 1.76257324 | +0.00087009 |
| 1.76245117 | 1.76257324 | 1.76251221 | +0.00017919 |
| 1.76245117 | 1.76251221 | 1.76248169 | −0.00016624 |
| 1.76248169 | 1.76251221 | 1.76249695 | +0.00000647 |
| 1.76248169 | 1.76249695 | 1.76248932 | −0.00007989 |
| 1.76248932 | 1.76249695 | 1.76249313 | −0.00003671 |
| 1.76249313 | 1.76249695 | 1.76249504 | −0.00001512 |
| 1.76249504 | 1.76249695 | 1.76249599 | −0.00000432 |
| 1.76249599 | 1.76249695 | 1.76249647 | +0.00000107 |
| 1.76249599 | 1.76249647 | 1.76249623 | −0.00000162 |
| 1.76249623 | 1.76249647 | 1.76249635 | −0.00000027 |
| 1.76249635 | 1.76249647 | 1.76249641 | +0.00000040 |
| 1.76249635 | 1.76249641 | 1.76249638 | +0.00000006 |
| 1.76249635 | 1.76249638 | 1.76249637 | −0.00000011 |
| 1.76249637 | 1.76249638 | 1.76249637 | −0.00000002 |
Po nekaj korakih postopka vidimo, da leži ničla funkcije f med številoma 1.76249637 in 1.76249638.
Dober približek za rešitev enačbe x3 + 2x = 9 je torej število 1.7624964.
Dobre in slabe strani bisekcije:
Bisekcija je dokaj preprosta numerična metoda, vendar pa je žal nekoliko dolgovezna. Za izračun treh decimalk moramo narediti približno deset korakov bisekcije.
Pri delu si lahko pomagamo s kalkulatorjem, še lažje pa gre, če imamo računalnik, ki se ga da programirati (zgornja tabela je narejena s programom v programskem jeziku BASIC).
Bisekcija je uporabna samo za iskanje ničel, v katerih zvezna funkcija spremeni predznak. Ničel sode stopnje z bisekcijo ne moremo odkriti.
Metoda navadne iteracije
Metodo navadne iteracije uporabljamo za reševanje enačb oblike x = g(x).Če želimo rešiti enačbo drugačne oblike, jo moramo najprej preoblikovati v obliko x = g(x). To pomeni, da moramo na levi strani pustiti samo člen x, vse ostalo pa moramo prenesti na desno stran enačbe.
Poleg enačbe oblike x = g(x) potrebujemo še število x0, ki ga imenujemo začetni približek.
Začetni približek vstavimo v desno stran enačbe (v funkcijo g) in dobljeni rezultat označimo x1.
Potem x1 vstavimo v desno stran enačbe in dobljeni rezultat označimo x2.
Nato x2 vstavimo v desno stran enačbe in dobljeni rezultat označimo x3 in tako naprej. Torej:
x1 = g(x0)
x2 = g(x1)
x3 = g(x2)
x4 = g(x3)
x5 = g(x4)
⋮
xn+1 = g(xn)
⋮
Pri tem ves čas ponavljamo isti postopek: dani približek vstavimo v desno stran enačbe in dobimo naslednji približek. Ime metode izvira iz latinske besede iteratio, ki pomeni ponavljanje.
Formula xn+1 = g(xn) se imenuje iteracijska formula. Z iteriranjem (ponavljanjem) te formule dobimo zaporedje približkov:
x0, x1, x2, x3, x4, …, xn, …
-
Če imamo srečo, zaporedje približkov konvergira (se približuje) k rešitvi enačbe.
Konvergenco spoznamo po tem, da so razlike med zaporednimi približki vedno manjše.
V tem primeru lahko dobimo z nadaljnim iteriranjem vedno boljše približke za rešitev enačbe.
-
Lahko pa se zgodi tudi, da zaporedje približkov ne konvergira: razlike med zaporednimi približki se ne manjšajo ampak ostajajo enake ali se celo večajo.
V tem primeru nas iteracija ne pripelje do rešitve enačbe.
Kadar zaporedje približkov ne konvergira, imamo na voljo dve možnosti:- izberemo lahko drug začetni približek in ga vstavimo v isto iteracijsko formulo, ali pa
- enačbo preoblikujemo na drug način in tako dobimo drugo iteracijsko formulo. Pozor: še zmerom moramo upoštevati obliko x = g(x).
Rešimo enačbo:
x3 + 2x = 9
Enačbo moramo preoblikovati v obliko x = g(x). To lahko storimo tako, da x3 prenesemo na desno in nato enačbo delimo z 2:
x3 + 2x = 9
2x = 9 − x3
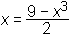
To obliko enačbe bomo uporabili kot iteracijsko formulo. Izberimo še začetni približek x0 = 0 in izračunajmo naslednje približke:
x0 = 0
x1 = 4.5
x2 = −41.0625
x3 = 34622.83411
x4 = …
Že po nekaj korakih vidimo, da zaporedje ne konvergira (razlike med členi se večajo). Po tej poti torej ne bomo prišli do rešitve.
Zato se odločimo, da bomo enačbo preoblikovali na drug način:
x3 + 2x = 9
x3 = 9 − 2x
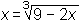
Zdaj to obliko enačbe uporabimo kot iteracijsko formulo. Izberimo isti začetni približek x0 = 0 in izračunajmo (s kalkulatorjem) naslednje približke:
x0 = 0
x1 = 2.080083823
x2 = 1.691518581
x3 = 1.777599217
x4 = 1.759249160
x5 = 1.763192990
x6 = 1.762346863
x7 = 1.762528463
x8 = 1.762489490
x9 = 1.762497854
x10 = 1.762496059
x11 = 1.762496445
x12 = 1.762496362
x13 = 1.762496380
x14 = 1.762496376
x15 = 1.762496377
x16 = 1.762496376
x17 = 1.762496376
Kot vidimo, se razlike med približki manjšajo, torej zaporedje konvergira. Zadnji štirje približki se ujemajo v vseh decimalkah razen v zadnji. Če postopek nadaljujemo, pa dobimo ujemanje v vseh decimalkah, ki jih izpiše kalkulator.
To pomeni, da smo prišli do rešitve enačbe. Zadnja decimalka je lahko nezanesljiva zaradi zaokrožanja, ostale pa upoštevamo in smiselno zaokrožimo.
Dober približek za rešitev enačbe x3 + 2x = 9 je torej število 1.76249638.
Dobre in slabe strani iteracijske metode:
Dobra stran te metode je preprostost. S kalkulatorjem lahko po metodi iteracije zelo hitro rešimo (skoraj) vsako enačbo. Žal pri tem ne vemo, ali ima enačba še kakšno drugo rešitev.
Slaba lastnost iteracijske metode je nezanesljivost: ko začnemo s postopkom, ne vemo, ali nas bo zaporedje približkov res pripeljalo do rešitve. Iz višje matematike je znano, da zaporedje približkov konvergira, če v okolici rešitve velja |g'(x)| < 1, vendar se ta pogoj v praksi le redko uporablja. Ponavadi je bolj enostavno, če preverimo konvergenco tako, da izračunamo prvih nekaj približkov.
Tangentna metoda
Tangentno metodo uporabljamo za iskanje ničel funkcije oziroma za reševanje enačbe oblike f (x) = 0.Če želimo rešiti enačbo drugačne oblike, lahko vse člene prenesemo na levo stran in dobimo obliko f (x) = 0.
Kot vemo, se tangenta na graf funkcije f v okolici dane točke zelo malo razlikuje od grafa funkcije.
Zato lahko uporabimo naslednji premislek: Naj bo x0 približek za ničlo funkcije f. Izračunajmo odvod in zapišimo tangento na graf funkcije f v točki x0. Ker se tangenta zelo malo razlikuje od grafa funkcije, se tudi ničla tangente zelo malo razlikuje od ničle funkcije. Za naslednji približek zato vzamemo število x1, ki je ničla te tangente.
Po enakem postopku dobimo naslednji približek x2 (zapišemo tangento v točki x1 in poiščemo ničlo te tangente).
Če nadaljujemo z istim postopkom, dobimo še nadaljne približke: x3, x4, x5, …, xn, …
Izkaže se, da dani približek xn z naslednjim približkom xn+1 povezuje naslednja zveza:
To je iteracijska formula, s katero dobimo zaporedje približkov.
Če je x0 dober začetni približek, potem dobljeno zaporedje približkov zelo hitro konvergira k rešitvi enačbe, zato tangentno metodo imenujemo tudi metoda pospešene iteracije. Po Isaacu Newtonu jo imenujemo tudi Newtonova metoda.
Zgled:
Rešimo enačbo:
x3 + 2x = 9
Enačbo najprej preoblikujemo v obliko:
x3 + 2x − 9 = 0
To pomeni, da iščemo ničle funkcije:
f (x) = x3 + 2x − 9
Izračunajmo odvod:
f '(x) = 3x2 + 2
In zdaj lahko zapišemo iteracijsko formulo (zaradi krajšega zapisa indekse pri iksih izpustimo):
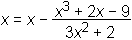
Izberimo začetni približek x0 = 0 in izračunajmo (s kalkulatorjem) naslednje približke.
x0 = 0
x1 = 4.5
x2 = 3.047808765
x3 = 2.197144764
x4 = 1.833064968
x5 = 1.764734233
x6 = 1.762498713
x7 = 1.762496376
x8 = 1.762496376
Pri prvih korakih bi morda pomislili, da zaporedje sploh ne konvergira. To je posledica dejstva, da začetni približek x0 = 0 v resnici ni zelo dober približek za rešitev enačbe.
Ko pridemo do približka x4 (ki je že zelo blizu rešitve), se začne pospešena konvergenca in v nekaj korakih pridemo do ujemanja v vseh decimalkah, ki jih izpiše kalkulator. Smiselno zaokrožimo in zapišemo rešitev:
Dober približek za rešitev enačbe x3 + 2x = 9 je torej število 1.76249638.
Dobre in slabe strani tangentne metode:
Dobra stran te metode je hitrost: tangentna metoda ponavadi pripelje do rešitve hitreje kot metoda navadne iteracije. Žal tudi pri tangentni metodi ne vemo, ali ima enačba še kakšno drugo rešitev. Pri iskanju drugih rešitev si pomagamo tako, da izberemo več različnih začetnih približkov.
Numerične metode običajno uporabljamo samo v obsegu realnih števil. Tangentno metodo lahko uporabimo tudi v kompleksnem: za začetni približek lahko izberemo poljubno kompleksno število in dobimo zaporedje približkov, ki konvergira h kompleksni rešitvi (seveda potrebujemo kalkulator ali računalniški program, ki zna računati s kompleksnimi števili).
Slaba lastnost tangentne metode: V iteracijski formuli v imenovalcu nastopa odvod funkcije f. Kadar je odvod enak 0, tangentna metoda odpove (problem deljenja z 0). To pomeni, da s tangentno metodo ne moremo poiskati ničel višje stopnje: dvojnih, trojnih ničel itd.
| Kazalo poglavij | Dodatek 1 | Kazalo simbolov | Abecedno kazalo |