Standardni in nestandardni koordinatni sistem

V matematiki ponavadi uporabljamo pravokotni koordinatni sistem, ki ima na obeh (oziroma na vseh treh) oseh enako velike enote. Imenujemo ga standardni pravokotni koordinatni sistem.

Včasih pa se odločimo, da izberemo na ordinatni osi drugačne enote kot na abscisni osi (v prostoru pa lahko izberemo še tretjo vrsto enot za aplikatno os). Tak koordinatni sistem imenujemo nestandardni pravokotni koordinatni sistem.

Poglejmo si nekaj razlik med njima in poskusimo ugotoviti, kdaj je bolje uporabiti standardni in kdaj nestandardni koordinatni sistem.

Prednosti standardnega koordinatnega sistema

Glavni razlog, zakaj se v matematiki praviloma odločamo za standardni koordinatni sistem, je v njegovi večji uporabnosti. Kar precej formul, enačb in postopkov, ki smo jih spoznali v tem priročniku, velja samo v standardnem koordinatnem sistemu.
Opozoriti velja na dejstvo, da te formule najdemo tudi v drugih matematičnih priročnikih in učbenikih, vendar pa v knjigah običajno ne piše, v kakšnem koordinatnem sistemu formule veljajo.

Formule in postopki ravninske geometrije:

V standardnem koordinatnem sistemu ima simetrala lihih kvadrantov enačbo y = x, simetrala sodih kvadrantov pa ima enačbo y = −x.
V nestandardnem koordinatnem sistemu to ne velja: premici y = x in y = −x nista simetrali. Enačbi simetral sta v nestandardnem koordinatnem sistemu odvisni od izbire enot.
Spodnji sliki prikazujeta simetralo lihih kvadrantov v standardnem in v nestandardnem koordinatnem sistemu
V standardnem koordinatnem sistemu sta grafa inverznih funkcij f in f ⁻¹ med seboj zrcalna glede na simetralo lihih kvadrantov y = x.
V nestandardnem koordinatnem sistemu grafa inverznih funkcij nista zrcalna niti glede na simetralo lihih kvadrantov niti glede na premico y = x.
V standardnem koordinatnem sistemu uporabljamo enake enote na vodoravni in na navpični osi. Logično lahko uporabimo enake enote tudi na poljubni (poševni) premici in v teh enotah izmerimo razdaljo med poljubnima dvema točkama. Za razdaljo med točkama A in B v standardnem koordinatnem sistemu velja formula:

V nestandardnem koordinatnem sistemu seveda nastopi problem že, ko hočemo izbrati enote za razdaljo merjeno po poševni premici. Če ne uporabljamo enakih enot za merjenje v vseh smereh, zgornja formula sploh nima smisla.
V standardnem koordinatnem sistemu lahko izračunamo naklonski kot premice s smernim koeficientom k po naslednji formuli:
tg α = k
V nestandardnem koordinatnem sistemu ta formula ne velja. Če računamo po tej formuli, dobimo popolnoma napačen rezultat.
V standardnem koordinatnem sistemu lahko izračunamo kot med dvema premicama po formuli:

V nestandardnem koordinatnem sistemu ta formula ne velja. Če računamo po tej formuli, dobimo popolnoma napačen rezultat.
V standardnem koordinatnem sistemu velja za smerna koeficienta pravokotnih premic naslednja zveza (pogoj pravokotnosti):

V nestandardnem koordinatnem sistemu ta pogoj ne velja.
V standardnem koordinatnem sistemu ima krožnica enačbo:
x² + y² = r ² oziroma (x − p)² + (y − q)² = r ²
V nestandardnem koordinatnem sistemu zgoraj zapisani enačbi ne predstavljata krožnice pač pa elipso.
V standardnem koordinatnem sistemu lahko izračunamo ploščino trikotnika ΔABC po naslednji formuli:
S o_r =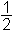 ( x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂) ) oziroma

V nestandardnem koordinatnem sistemu zgornji formuli ob običajnih predpostavkah ne veljata. Lahko pa ustrezno popravimo definicijo ploščine. Običajna definicija pravi, da je ploščina število enotskih kvadratkov, s katerimi lahko popolnoma prekrijemo dani lik. Če namesto enotskih kvadratkov vzamemo enotske pravokotnike, ki imajo za vodoravno stranico enoto na abscisni osi, za navpično stranico pa enoto na ordinatni osi, potem obe zgornji formuli veljata.
V standardnem koordinatnem sistemu lahko izračunamo ploščino lika pod grafom pozitivne funkcije po formuli:
S =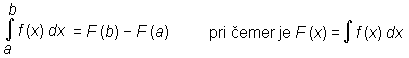
V nestandardnem koordinatnem sistemu to velja samo, če prilagodimo definicijo ploščine na enak način kot zgoraj.

Formule in postopki prostorske geometrije:

V standardnem koordinatnem sistemu lahko izračunamo razdaljo med točkama A in B v prostoru po formuli:

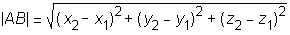
V nestandardnem koordinatnem sistemu ta formula ne velja.
V standardnem koordinatnem sistemu lahko izračunamo dolžino vektorja = (a₁, a₂, a₃) po formuli:

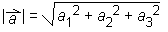
V nestandardnem koordinatnem sistemu ta formula ne velja. V višji matematiki to formulo včasih vseeno uporabljamo tudi v nestandardnem koordinatnem sistemu. Rezultat, ki ga dobimo po tej formuli, imenujemo norma vektorja. Norma je povezana z dolžino, vendar pa ni isto kot dolžina v običajnem pomenu besede.
V standardnem koordinatnem sistemu lahko izračunamo skalarni produkt po dveh formulah in po obeh formulah dobimo isti rezultat:
= || || cos φ
= a₁b₁ + a₂b₂ + a₃b₃
V nestandardnem koordinatnem sistemu dobimo po zgornjih formulah različna rezultata. V nestandardnem koordinatnem sistemu za definicijo skalarnega produkta ponavadi vzamemo drugo formulo (prva pa je potem neveljavna).
V standardnem koordinatnem sistemu lahko izračunamo kot med vektorjema in po formuli:

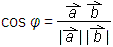
V nestandardnem koordinatnem sistemu po tej formuli ne moremo izračunati kota med vektorjema. V višji matematiki se jo včasih vseeno uporablja, vendar rezultat ni kót v običajnem pomenu besede.
V standardnem koordinatnem sistemu sta vektorja pravokotna, če je njun skalarni produkt enak 0. Če je skalarni produkt pozitiven, vektorja oklepata ostri kot, če je skalarni produkt negativen, pa oklepata topi kot.
V nestandardnem koordinatnem sistemu to ni res.
Zgoraj zapisano ne velja samo za prostorske, pač pa tudi za ravninske vektorje.
Zgled: Izračunajmo kot med vektorjema = (1,3) in = (1,−2).
Po običajnih postopkih izračunamo obe dolžini in skalarni produkt: || = √10, || = √5, = −5.
Po formuli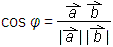 dobimo kot med vektorjema: φ = 135°.
Če vektorja narišemo v standardnem koordinatnem sistemu, vidimo da kot res meri 135° (lahko ga izmerimo s kotomerjem).
V nestandardnem koordinatnem sistemu pa kot očitno ne meri 135° (na sliki vidimo, da lahko vektorja ob primerni izbiri enot oklepata celo ostri kot, čeprav je skalarni produkt negativen).

Prednosti nestandardnega koordinatnega sistema

V matematiki

Uporaba nestandardnega koordinatnega sistema je zares smiselna, če želimo narisati graf funkcije, ki je v eni smeri močno razpotegnjen v drugi smeri pa stisnjen.
Zgled za to je graf polinoma p(x) = x³(x − 3)²(x + 2):

Polinom

V fiziki

V fiziki (in drugih naravoslovnih znanostih) običajno uporabljajo nestandardni koordinatni sistem takrat, ko na koordinatni osi nanašajo različni fizikalni količini, ki imata tudi različne enote, npr. pot in čas. V takih primerih zgoraj zapisane formule itak ne pridejo v poštev.

Posebna izjema pri tem je ploščina oziroma formule povezane s ploščino. V fiziki je namreč kar nekaj količin, ki jih lahko povežemo s ploščino lika pod grafom neke funkcije.
Zgled: Spodnji graf prikazuje, kako se sila (F) spreminja s potjo (s). Delo (A), ki ga pri tem opravimo, je enako ploščini lika pod grafom funkcije.

Delo kot ploščina

Pri tem fiziki ponavadi zamolčijo, za kakšno ploščino gre. Ne gre namreč za običajno matematično ploščino, ki ima za enote kvadratke s stranico 1, pač pa (kot smo omenili že zgoraj) za posebno ploščino, kjer so enote pravokotniki, ki imajo vodoravno stranico dolgo 1 vodoravno enoto, navpično stranico pa dolgo 1 navpično enoto. Šele če upoštevamo to predpostavko, je ploščina lika na zgornji sliki res enaka delu (A).