Osnove statistike

Statistika je veda, ki se ukvarja z urejanjem velikega števila podatkov.

Statistično raziskavo opravimo na veliki množici elementov (oseb, živali, predmetov,...). Vsak posamezni element imenujemo statistična enota, celotno množico pa imenujemo populacija.
Če je populacija prevelika, raziskavo opravimo na vzorcu - na delu populacije. Pri tem poskušamo zagotoviti reprezentativnost vzorca. Vzorec je reprezentativen, če so rezultati raziskave na vzorcu enaki, kot bi bili rezultati raziskave na celotni populaciji.
Število statističnih enot, ki jih zajamemo v raziskavi, ponavadi označujemo s črko N (numerus).

Lastnost, ki jo preučujemo pri posamezni statistični enoti, se imenuje statistični znak.
Statistični znaki so lahko numerični (se izračajo s števili) ali nenumerični (se izražajo drugače). Numerični statistični znaki so lahko diskretni (imajo samo nekaj posameznih možnih rezultatov) ali zvezno porazdeljeni (lahko dosežejo poljubno vrednost na nekem intervalu).

Frekvenca nam pove, kako pogosto v raziskavi naletimo na določeno vrednost statističnega znaka. Absolutna frekvenca pomeni število enot (npr. oseb), ki imajo določeno vrednost statističnega znaka; relativna frekvenca pa nam pove kolikšen delež oziroma kolikšen procent vseh enot (oseb) ima določeno vrednost statističnega znaka.

Statistični parametri so splošne lastnosti, ki veljajo za populacijo kot celoto in jih dobimo kot rezultat statistične raziskave.

Prikaz podatkov

Statistične podatke prikazujemo s tabelami in z grafikoni.

Zgled:
V razredu je 30 učencev. Od tega so 3 nezadostni, 7 zadostnih, 10 dobrih, 6 prav dobrih in 4 odlični.

Rezultate zapišemo v tabelo absolutnih frekvenc:

ocena	absolutna frekvenca
1	3
2	7
3	10
4	6
5	4

Te podatke ponazorimo še s tremi vrstami grafikonov, ki jih najpogosteje uporabljamo.

Frekvenčni poligon
Na vodoravno os nanašamo različne vrednosti statističnega znaka (v tem primeru različne ocene), na navpično os pa frekvence (tj. število učencev, ki imajo določeno oceno).
Histogram ali stolpčni diagram
Na vodoravno os nanašamo različne vrednosti statističnega znaka (v tem primeru različne ocene), na navpično os pa frekvence (tj. število učencev, ki imajo določeno oceno).
Krožni diagram ali frekvenčni kolač
Vsako vrednost statističnega znaka predstavlja krožni izsek. Velikost krožnega izseka je premo sorazmerna s frekvenco (tj. s številom učencev, ki imajo določeno oceno).

Povprečje in standardni odklon

Povprečje ali povprečna vrednost je najpombembnejši statistični parameter. Povprečje je mera za srednjo vrednost statističnega znaka.

Če označimo različne vrednosti statističnega znaka z x₁, x₂, x₃, ..., x_n in njihove frekvence s f₁, f₂, f₃, ..., f_n, potem povprečno vrednost izračunamo po formuli:

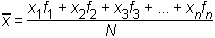
oziroma (če uporabimo zapis s sumacijskim znakom):
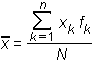
Povprečje

(Pri tem je N = f₁ + f₂ + f₃ + … + f_n)

Drugi najpomembnejši statistični parameter je standardni odklon ali standardna deviacija (σ). Pove nam, za koliko vrednosti statističnega znaka odstopajo od povprečja. Pravimo tudi, da je standardni odklon mera za razpršenost porazdelitve vrednosti.

Standardni odklon izračunamo po formuli:

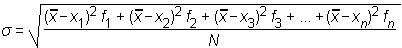
oziroma (če uporabimo zapis s sumacijskim znakom):
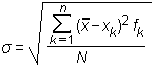
Standardni odklon

Namesto standardnega odklona se kot mero razpršenosti včasih uporablja tudi kvadrat standardnega odklona: σ². To število se imenuje varianca ali disperzija.

Mediana in kvartili

Mediana (ali središčnica) je statistični parameter, ki (podobno kot povprečje) podaja srednjo vrednost statističnega znaka.
Mediano M določimo tako, da vrednosti statističnega znaka najprej uredimo po velikosti (od najmanjše do največje) in zapišemo v obliki zaporedja členov. Mediana je vrednost, ki nastopa v sredini tako dobljenega zaporedja (število manjših členov je enako kot število večjih členov). Ločimo dva primera:

Če je členov liho mnogo, je mediana kar vrednost srednjega člena.
Zgled: Šolsko nalogo je pisalo 19 učencev. Štirje učenci so dobili oceno 1, pet učencev oceno 2, sedem učencev oceno 3, dva oceno 4 in eden oceno 5. Ocene najprej zapišemo po velikosti:
1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 4, 4, 5.
V sredini tega zaporedja je ocena 3. Torej je mediana enaka M = 3.
Če je členov sodo mnogo, pa je mediana aritmetična sredina srednjih dveh členov.
Zgled: Šolsko nalogo je pisalo 20 učencev. Štirje učenci so dobili oceno 1, šest učencev oceno 2, sedem učencev oceno 3, dva oceno 4 in eden oceno 5. Ocene najprej zapišemo po velikosti:
1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 4, 4, 5.
V sredini tega zaporedja sta dve števili: 2 in 3. Mediana je aritmetična sredina teh dveh števil, torej M = 2,5.

Mediana razdeli zaporedje vrednosti na dva enako velika dela. Če vsakega od teh dveh delov spet razdelimo na dva enaka dela, potem dobljene delilne točke imenujemo kvartili.

Zgled: Stehtali smo vse učence v razredu in zapisali njihove mase od najmanjše do največje:
    45, 48, 51, 52, 53, 55, 56, 59, 59, 60, 61, 61, 62, 63, 63, 66, 68, 70, 77.

Števila Q₁ = 53, Q₂ = 60 in Q₃ = 63 so kvartili. Drugi kvartil je enak mediani: Q₂ = M.

Razpon od prvega do tretjega kvartila imenujemo medčetrtinski razmik ali kvartilni razmik (QR). To število uporabljamo kot mero za razpršenost vrednosti statističnega znaka.
Druga mera razpršenosti pa je razpon od najmanjše do največje vrednosti statističnega znaka. To število imenujemo variacijski razmik (VR).

    QR = Q₃ − Q₁
    VR = x_max − x_min

Mediano, kvartile in variacijski razmik pogosto slikovno upodobimo na posebni vrsti diagrama, ki mu rečemo kvartilni diagram ali škatla z brki.

Zgled: narišimo škatlo z brki za zgoraj navedeno porazdelitev mas učencev:
    45, 48, 51, 52, 53, 55, 56, 59, 59, 60, 61, 61, 62, 63, 63, 66, 68, 70, 77.

"Škatla" (pravokotnik v sredini) ponazarja območje od prvega do tretjega kvartila. Na škatli je označena tudi mediana. Oba "brka" (leva in desna črta) pa ponazarjata variacijski razmik: leva črta sega do minimalne, desna pa do maksimalne vrednosti.

Modus

Modus (ali gostiščnica) je statistični parameter, ki nam pove, katera vrednost v porazdelitvi nastopa največkrat. (Če več vrednosti nastopa enako pogosto, ima porazdelitev več modusov.)

Zgled: Učenec je dobil letos pri matematiki ocene:
1, 2, 2, 2, 3, 3, 4, 5, 5.
V zaporedju največkrat nastopa število 2, torej je modus enak Mo = 2.

Povprečje, mediana in modus so tri različne mere za srednjo vrednost. Če je porazdelitev vrednosti statističnega znaka normalna, se ta tri števila le malo razlikujejo med sabo. Pri bolj čudnih porazdelitvah pa so lahko razlike med temi tremi števili zelo velike. Od podatkov in od njihovega dejanskega pomena je odvisno, katero od teh treh števil je najbolj primerno izbrati za smiselen opis dane porazdelitve.

Zgled: V podjetju je zaposlenih devet ljudi: štirje laboranti dobivajo plačo po 1000 evrov na mesec, dva tehnika dobita po 2000, glavni inženir dobi 3000, pomočnik direktorja dobi 5000 evrov na mesec, direktor pa dobi 20000 evrov na mesec.

Če plače uredimo po velikosti, dobimo naslednje zaporedje:
1000, 1000, 1000, 1000, 2000, 2000, 3000, 5000, 20000.

Modus je enak 1000, mediana je enaka 2000, povprečje pa je 4000.
Mojster Miha se zanima za službo v tem podjetju, zanima pa ga, kakšno mesečno plačo lahko pričakuje. Bralec naj sam premisli, katero od zgornjih treh števil to najbolje opisuje.