Kazalo poglavij

Naravna in cela števila

Realna števila

Abecedno kazalo

Racionalna števila

Ulomek je zapis oblike .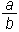

Sestavljen je iz celega števila a, ki ga imenujemo števec, in iz celega števila b  (b ≠ 0), ki ga imenujemo imenovalec, ter iz ulomkove črte.

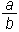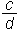Racionalna števila so števila, ki jih lahko zapišemo z ulomki. Pri tem ulomka in predstavljata isto racionalno število, če velja zveza: a d = b c, torej: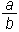

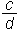   =   ⇔   a d = b c

Če števec in imenovalec ulomka pomnožimo z istim od 0 različnim celim številom, dobljeni ulomek predstavlja isto racionalno število kot prvotni ulomek. Ta postopek imenujemo razširjanje ali širjenje ulomka.
Zgled:
  

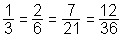
Če števec in imenovalec ulomka delimo s poljubnim skupnim deliteljem teh dveh števil, dobljeni ulomek predstavlja isto racionalno število kot prvotni ulomek. Ta postopek imenujemo krajšanje ulomka. Če ima ulomek za števec in imenovalec tuji števili, pravimo, da je okrajšan.
Zgled:
  

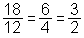
Množico racionalnih števil označimo:
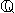
Uporabljamo tudi oznaki:
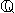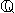  ⁺ = množica vseh pozitivnih racionalnih števil
  ⁻ = množica vseh negativnih racionalnih števil

Torej velja: 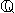   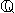= ⁻ ∪ {0} ∪ ⁺

Poljubno celo število lahko zapišemo kot ulomek z imenovalcem 1, torej so cela števila tudi elementi množice racionalnih števil in velja:
   ⊂ ⊂

Računanje z ulomki

Racionalna števila uvedemo, ker v množici celih (in tudi naravnih) števil ne moremo vedno deliti. V množici racionalnih števil je možno deliti poljubno število s poljubnim od nič različnim številom.
Tako lahko v množici seštevamo, odštevamo, množimo in delimo z eno samo omejitvijo: deljenje z 0 ni mogoče.
Pri tem si pomagamo z naslednjimi pravili:

  

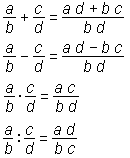
Torej:
Seštevamo (odštevamo) tako, da najprej poiščemo skupni imenovalec, potem pa seštejemo (odštejemo) oba števca.
Množimo tako, da zmnožimo med sabo oba števca in potem še oba imenovalca.
Delimo tako, da prvi ulomek pomnožimo z obratno vrednostjo drugega ulomka.
Obratna vrednost je ulomek, ki ga dobimo, če zamenjamo števec in imenovalec. Obratno vrednost racionalnega števila x označimo tudi x⁻¹, oziroma:
  

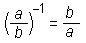
Za računske operacije v množici racionalnih števil veljajo naslednji zakoni oziroma aksiomi (za ∀a, b, c ∈ ):

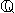a + b = b + a	komutativnostni zakon (za seštevanje)
a + (b + c) = (a + b) + c	asociativnostni zakon (za seštevanje)
a + 0 = a	zakon o nevtralnem elementu (za seštevanje)
a + (−a) = 0	zakon o inverznem (nasprotnem) elementu (za seštevanje)
a b = b a	komutativnostni zakon (za množenje)
a (b c) = (a b) c	asociativnostni zakon (za množenje)
a 1 = a	zakon o nevtralnem elementu (za množenje)
a a−1 = 1 (za a ≠ 0)	zakon o inverznem (obratnem) elementu (za množenje)
a (b + c) = a b + a c	distributivnostni zakon (za seštevanje in množenje)

V zgoraj zapisanih zakonih odštevanje in deljenje ne nastopata, ker odštevanje pomeni prištevanje nasprotne vrednosti (torej: a − b = a + (−b)), deljenje pa pomeni množenje z obratno vrednostjo (torej: a : b = a b⁻¹).

Decimalni zapis racionalnega števila

Racionalna števila lahko zapišemo tudi z decimalnim mestnim zapisom. Pri tem prvo decimalno mesto za decimalno vejico (ali piko) pomeni desetinke, drugo mesto stotinke, tretje mesto tisočinke, ...
Primer:
  12,3456 = 12 celih + 3 desetinke + 4 stotinke + 5 tisočink + 6 desettisočink

Ulomek preoblikujemo v decimalni zapis z decimalnim deljenjem (števec delimo z imenovalcem).
Pri tem se lahko zgodi, da se deljenje po nekaj korakih izide, npr.:
  

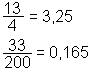
Kadar se deljenje ne izide, pa vedno pride do ponavljanja neke skupine decimalk, npr.:
  

Ponavljajočo skupino decimalk imenujemo perioda in jo označimo z vodoravno črto zgoraj.
V primeru, ko se deljenje po nekaj korakih izide in je decimalni zapis končen, lahko štejemo, kot da od tega mesta naprej sledijo same ničle - torej lahko tudi v tem primeru govorimo o ponavljanju oziroma periodičnosti.
Velja ugotovitev: Vsako racionalno število lahko zapišemo z neskončnim periodičnim decimalnim zapisom.

Razmerje, delež, procent, promil

Razmerje opisuje odnos med danimi količinami.
Dvočleno (ali enostavno) razmerje a : b nam pove, da prva količina znaša a enot, druga pa b enot. Enote so pri tem lahko precej poljubne.

Veččleno (ali podaljšano) razmerje a : b : c :   · · ·   : d nam pove, da prva količina znaša a enot, druga b enot, tretja c enot, ... in zadnja d enot.

Zgled: V razredu je 12 fantov in 18 deklet. To pomeni, da je razmerje med njimi enako 12 : 18 (če za enoto izberemo 1 osebo), ali v okrajšani obliki:
   f : d = 2 : 3
   (Za mersko enoto izberemo 6 oseb. Količina fantov je potem 2 enoti, količina deklet pa je 3 enote.)

Kot vidimo iz zgornjega zgleda, lahko razmerja razširjamo in krajšamo (podobno kot ulomke), tako da vse člene razmerja pomnožimo ali delimo z istim od 0 različnim številom.

Zgled: V škatli je 8 rdečih, 16 modrih in 12 zelenih žogic. Razmerje med rdečimi, modrimi in zelenimi je enako:
   r : m : z = 8 : 16 : 12 = 2 : 4 : 3

Razmerje med delom in celoto imenujemo delež. Delež običajno zapišemo v obliki ulomka, možen pa je tudi zapis v drugih oblikah. Delež izražen v stotinah imenujemo procentni (odstotni) delež ali na kratko procent (oznaka %), delež izražen v tisočinah pa imenujemo promilni delež ali na kratko promil (oznaka ‰).

Zgled: V razredu je 12 fantov in 18 deklet. To pomeni, da je vseh skupaj 12 + 18 = 30. Delež fantov je razmerje med številom fantov in številom vseh učencev, torej
  12 : 30 = 2 : 5 = 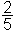  (beri: delež fantov v razredu je )

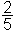To lahko zapišemo tudi v drugih oblikah:
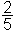   = 0,4 = 0,40 = 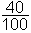= 40% (delež fantov v razredu je 40 stotin oziroma 40 procentov)

        = 0,400 = 400‰ (delež fantov v razredu je 400 tisočin oziroma 400 promilov)

Povečanje (zmanjšanje) za p%

Povečanje dane količine x₀ za p% pomeni, da dani količini x₀ prištejemo še p% od te količine, torej:
   x₁ = x₀ + p% od x₀.
Če ta izraz polepšamo, dobimo formulo:
  

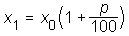
Z isto formulo lahko izračunamo tudi zmanjšanje dane količine x₀ za p%, upoštevamo samo negativni predznak (zmanjšanje za p% je isto kot zvečanje za −p%).

Kazalo poglavij

Naravna in cela števila

Realna števila

Abecedno kazalo