Verjetnostni račun

Dogodki

Verjetnostni poskus je poskus, katerega rezultat je odvisen od naključja.
Osnovne rezultate verjetnostnega poskusa imenujemo izidi.

Dogodek je vsak pojav, ki se v verjetnostnem poskusu lahko zgodi. Dogodek lahko zapišemo kot množico izidov, ki so za ta dogodek ugodni.

Zgled:
Poskus = met običajne igralne kocke
Izidi = 1, 2, 3, 4, 5, 6
Nekaj primerov dogodkov, ki jih lahko opazujemo v tem poskusu:

A: pade šestica	A = {6}
B: pade liho število	B = {1,3,5}
C: pade manj kot 5	C = {1,2,3,4}
D: pade več kot 3	D = {4,5,6}

Zaradi sistematičnosti štejemo za dogodka tudi naslednja posebna primera:

Nemogoč dogodek je dogodek, ki se nikoli ne zgodi. Označimo ga N. Predstavlja ga prazna množica izidov, torej: N = { }.
Gotov dogodek je dogodek, ki se zgodi vedno. Označimo ga G. Predstavlja ga univerzalna množica - to je množica vseh možnih izidov danega poskusa.

Računanje z dogodki

Produkt ali presek dogodkov A in B je dogodek, ki se zgodi, kadar se zgodita dogodka A in B oba hkrati. Če dogodka predstavimo z množicama ugodnih izidov, produktu dogodkov ustreza presek množic.
Produkt oz. presek dogodkov označimo A B oziroma A ∩ B.

Če se dogodka A in B ne moreta zgoditi oba hkrati, pravimo, da sta nezdružljiva. Produkt nezdružljivih dogodkov je nemogoč dogodek: A B = N

Unija dogodkov A in B je dogodek, ki se zgodi, kadar se zgodi vsaj eden od danih dogodkov - ali A ali B ali oba. Če dogodka predstavimo z množicama ugodnih izidov, tej operaciji ustreza unija množic, zato uporabljamo tudi isto poimenovanje in isto oznako: A ∪ B.
Nekateri matematiki unijo dogodkov imenujejo tudi vsota dogodkov in jo označijo A + B. To poimenovanje se uporablja zlasti, kadar gre za unijo nezdružljivih dogodkov.

Nasprotni dogodek danega dogodka A je dogodek, ki se zgodi točno takrat, ko se dogodek A ne zgodi. Če dogodek A predstavimo z množico ugodnih izidov, nasprotnemu dogodku ustreza komplement množice A.
Nasprotni dogodek označimo A'.

Dogodek A je način dogodka B, če se vedno, kadar se zgodi A, hkrati zgodi tudi dogodek B. Če dogodka predstavimo z množicama ugodnih izidov, to pomeni, da je A podmnožica množice B.

Verjetnost dogodka

Imejmo verjetnostni poskus, ki ima vse izide enakovredne. To pomeni, da se pri velikem številu ponovitev tega poskusa vsi izidi pojavljajo (v povprečju) enako pogosto. V takem poskusu za dogodek A definiramo verjetnost z naslednjo definicijo:

Verjetnost dogodka A je razmerje med številom ugodnih izidov in številom vseh možnih izidov.
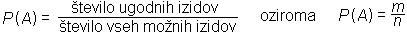
Definicija verjetnosti

Verjetnost nemogočega dogodka je enaka 0, verjetnost gotovega dogodka pa je enaka 1.
Verjetnost poljubnega dogodka leži na intervalu [0, 1].

Verjetnost nasprotnega dogodka:
  P(A') = 1 − P(A)    oziroma    P(A) + P(A') = 1

Verjetnost unije dogodkov (splošno):
  P(A ∪ B) = P(A) + P(B) − P(A B)

Verjetnost unije nezdružljivih dogodkov (A B = N):
  P(A ∪ B) = P(A) + P(B)

Če dogodek A ne vpliva na verjetnost dogodka B in obratno, pravimo, da sta dogodka A in B neodvisna.
Verjetnost produkta neodvisnih dogodkov:
  P(A B) = P(A) P(B)

Če sta dogodka A in B odvisna, potem je verjetnost dogodka B različna v primeru, če se je dogodek A zgodil ali ne. Verjetnost dogodka B v primeru, če se je dogodek A zgodil, imenujemo pogojna verjetnost dogodka B pri pogoju A in jo označimo P(B/A).
Verjetnost produkta odvisnih dogodkov je enaka:
  P(A B) = P(A) P(B/A)