Kazalo poglavij

Integral

Verjetnostni račun

Abecedno kazalo

Kombinatorika

Pravilo vsote:
Če imamo na voljo m možnosti iz prve skupine in n možnosti iz druge skupine, izbrati pa želimo točno eno možnost iz prve ali iz druge skupine, potem imamo na izbiro skupno m + n možnosti.

Pravilo produkta ali Osnovni izrek kombinatorike:
Če imamo na voljo m možnosti iz prve skupine in n možnosti iz druge skupine, izbrati pa želimo eno možnost iz prve in hkrati eno iz druge skupine, potem imamo na izbiro skupno m n možnosti.

Permutacije

Permutacije so razporeditve danih n elementov na n prostih mest.

Če so vsi elementi med seboj različni, so to permutacije brez ponavljanja.
Število permutacij brez ponavljanja izračunamo po formuli:
  P_n = n (n - 1) · · · 3 · 2 · 1

V formuli nastopa računska operacija »zmnoži vsa naravna števila od 1 do n«. To računsko operacijo imenujemo faktoriela ali fakulteta in jo označimo n !
Torej:   n ! = n (n - 1) · · · 3 · 2 · 1    oziroma   P_n = n !

(Opomba: Zaradi računskih razlogov definiramo faktorielo tudi za število 0 in sicer 0 ! = 1.)

Permutacije s ponavljanjem so permutacije elementov, ki niso vsi med sabo različni. Pri tem lahko nastopa celo več skupin med sabo enakih elementov. Recimo, da je v prvi taki skupini k₁ enakih elementov, v drugi k₂ enakih elementov, ..., v m-ti pa k_m enakih elementov. Potem število permutacij s ponavljanjem izračunamo po formuli:
  

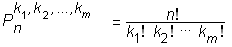
Variacije

Variacije brez ponavljanja so razporeditve n različnih elementov na r prostih mest. Pri tem je r < n, zato ostane nekaj elementov nerazporejenih.
Število variacij brez ponavljanja izračunamo po formuli:
  

Variacije s ponavljanjem so razporeditve, pri katerih poskušamo na r prostih mest razporediti elemente n različnih vrst. Pri tem se lahko element določene vrste v razporeditvi pojavi poljubno mnogokrat.
Število variacij s ponavljanjem izračunamo po formuli:
  

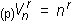
Kombinacije

Če pri variacijah zanemarimo vrstni red in opazujemo samo, kateri elementi so izbrani, dobimo kombinacije.

Kombinacije brez ponavljanja so izbire r (različnih) elementov izmed n različnih elementov, ki so na voljo.
Število kombinacij brez ponavljanja izračunamo po formuli:
  

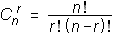
Izraz, ki nastopa na desni strani zgornje formule, lahko označimo tudi z binomskim simbolom:
  

Kombinacije s ponavljanjem dobimo, če pri variacijah s ponavljanjem zanemarimo vrstni red. To so torej izbire, kjer izbiramo r elementov izmed n, vendar pa lahko isti element izberemo tudi večkrat (poljubno mnogokrat).
Število kombinacij s ponavljanjem izračunamo po formuli:
  

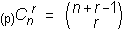
Kazalo poglavij

Integral

Verjetnostni račun

Abecedno kazalo