Integral

Nedoločeni integral

Nedoločeni integral je operacija, ki deluje obratno kot odvajanje. To pomeni, da je nedoločeni integral funkcije f enak tisti funkciji F, katere odvod je enak dani funkciji f. Nedoločeni integral funkcije f označimo ∫ f (x) dx. Torej velja:
  ∫ f (x) dx = F (x)    ⇔    F '(x) = f (x)

Funkcijo F, ki jo dobimo kot rezultat integriranja, imenujemo primitivna funkcija.
Ker je odvod konstanete enak 0, lahko primitivni funkciji prištejemo poljubno konstanto, pa bo njen odvod še vedno enak f (x).
To pomeni, da je rezultat nedoločenega integrala določen samo do aditivne konstante natančno. Zato tudi v zapisu rezultata običajno dodamo člen +C, torej:
  ∫ f (x) dx = F (x) + C

Osnovna pravila integriranja
  ∫ A f (x) dx = A ∫ f (x) dx
  ∫ (f (x) + g(x)) dx = ∫ f (x) dx + ∫ g(x) dx
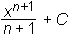  ∫ xⁿ dx = x^(n+1)/(n+1)

(za vsak n ∈

, n ≠ −1)
∫ 1/x

dx = tg x + C
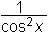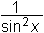∫ 1/sin2 x

dx = − ctg x + C

∫ e^x dx = e^x + C
∫ 1/(x2+1)

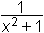dx = arc tg x + C

Določeni integral

Imejmo funkcijo f, ki je na intervalu [a, b] nenegativna. Izračunati želimo ploščino lika, ki ga omejuje graf funkcije f skupaj z abscisno osjo in z navpičnima premicama x = a in x = b.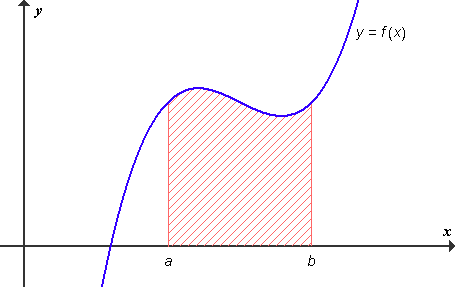

Izkaže se, da je ploščina tega lika enaka S = F (b) − F (a), pri čemer je funkcija F enaka nedoločenemu integralu dane funkcije f.
Zato se odločimo, da definiramo določeni integral funkcije f na intervalu [a, b] z Newton-Leibnizevo formulo:

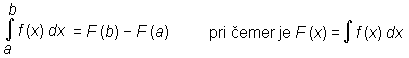
Če je funkcija f na intervalu [a, b] pozitivna ali enaka 0, je vrednost določenega integrala enaka ploščini lika, ki ga na tem intervalu omejujeta graf funkcije f in abscisna os.
Če je funkcija na tem intervalu negativna, je rezultat določenega integrala enak nasprotni vrednosti ploščine ustreznega lika.

Z določenim integralom lahko izračunamo tudi ploščino lika, ki ga omejujeta grafa dveh funkcij:

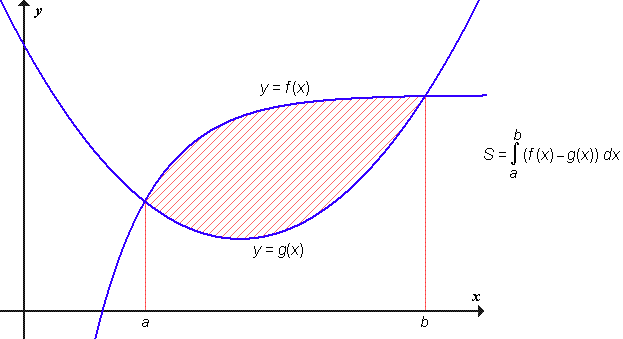
Lik med dvema krivuljama

Kazalo poglavij

Odvod

Kombinatorika

Abecedno kazalo