Odvod

Limita funkcije

Imejmo dano funkcijo f in realno število a. Zaporedje x_n naj konvergira proti številu a. Sestavimo drugo zaporedje y_n po pravilu: y_n = f (x_n).
Če zaporedje y_n vedno konvergira k istemu realnemu številu b (ne glede na to, kako izberemo zaporedje x_n, ki konvergira proti a), potem pravimo, da je število b limita funkcije f, ko gre x proti a.

To pomeni, da je limita funkcije vrednost, ki se ji približujejo rezultati funkcije, če se podatki približujejo številu a.
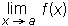
Limito funkcije f, ko gre x proti a, označimo: limita

Če se graf funkcije v okolici točke a ne pretrga, pravimo, da je funkcija v tej točki zvezna.

Velja:
Funkcija je v točki a zvezna, če in samo če je limita funkcije, ko gre x proti a, enaka funkcijski vrednosti v tej točki, torej:
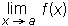Funkcija je v točki a zvezna ⇔ limita

= f (a)

Odvod funkcije

Tangenta na graf funkcije f v točki T(x, y) je premica, ki se v okolici te točke najbolj prilega grafu funkcije.
(Opomba: Tangenta na graf obstaja, samo če je graf v okolici dane točke gladek. V točkah, kjer se graf prelomi, tangenta ne obstaja.)

Odvod funkcije f v točki T(x, y) je smerni koeficient tangente na graf te funkcije v tej točki. Označimo ga f '(x).

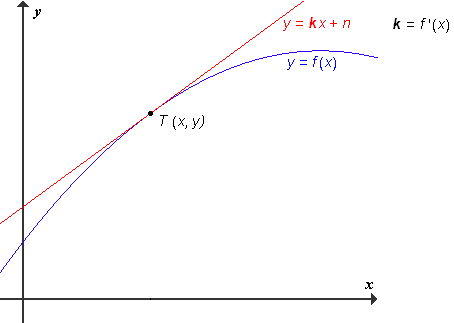
Geometrijski pomen odvoda

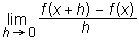
Računsko določimo odvod s pomočjo limite: f '(x) = Definicija odvoda

Ker je odvod enak smernemu koeficientu premice, ki se grafu funkcije zelo dobro prilega, nam odvod pove, kakšna je strmina grafa funkcije v dani točki.
Če je na nekem intervalu odvod funkcije pozitiven in kvečjemu v posameznih točkah enak 0, potem funkcija na tem intervalu narašča.
Če je na nekem intervalu odvod funkcije negativen in kvečjemu v posameznih točkah enak 0, potem funkcija na tem intervalu pada.

Naklonski kot grafa funkcije v dani točki definiramo kot naklonski kot tangente na graf te funkcije v tej točki in ga izračunamo po znani formuli:
tg α = k

Pravila odvajanja

Funkcija	Odvod

A f (x)	A f '(x)

f (x) + g(x)	f '(x) + g'(x)

f (x) g(x)	f '(x) g(x) + f (x) g'(x)



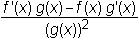f (g(x))	f '(g(x)) g'(x)

xⁿ	n x^n −1

sin x	cos x

cos x	− sin x

tg x

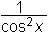ctg x

e^x	e^x

a^x	a^x ln a

ln x

log_a x

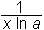Stacionarne točke

Stacionarna točka funkcije je točka, v kateri je odvod funkcije enak 0.
To pomeni, da je tangenta v stacionarni točki vodoravna.

Poznamo tri vrste stacionanih točk:

Lokalni minimum je najnižja točka v neki okolici. Spoznamo ga po tem, da funkcija levo od minimuma pada, desno pa narašča, torej je odvod funkcije levo od minimuma negativen, desno pa pozitiven.
Lokalni maksimum je najvišja točka v neki okolici. Spoznamo ga po tem, da funkcija levo od maksimuma narašča, desno pa pada, torej je odvod funkcije levo od maksimuma pozitiven, desno pa negativen.
Vodoravni prevoj je točka, v kateri je tangenta vodoravna, vendar pa ni niti minimum niti maksimum. Funkcija je v okolici vodoravnega prevoja monotona (samo narašča ali pa samo pada). Predznak odvoda se v vodoravnem prevoju ne spremeni.