Kazalo poglavij

Izjave

Naravna in cela števila

Abecedno kazalo

Množice

Množica je poljubna skupina elementov. Dejstvo, da množica M vsebuje element a, označimo:
  a ∈ M       (beri: a je element množice M, a pripada M)

Če a ni element množice M, pa to označimo:
  a  M       (beri: a ni element množice M, a ne pripada M)

Poseben primer množice je prazna množica - to je množica, ki ne vsebuje nobenega elementa.
Označimo jo s simbolom Ø ali { }.

Zapis množice

Množico lahko zapišemo na različne načine. Pri preprostih množicah, ki imajo malo elementov, uporabljamo zapis z naštevanjem elementov. Elemente pri tem ločimo z vejicami. Če je elementov neskončno mnogo, označimo nadaljevanje s tremi pikami. Primeri:
  A = {1, 2, 3, 4, 5, 6}
  B = {2, 4, 6, 8, 10, 12, ...}
  C = {..., −3, −1, 1, 3, 5, ...}

Uporabljamo tudi zapis z lastnostjo. Najprej navedemo oznako elementa, potem pa za podpičjem naštejejemo lastnosti, ki jih mora imeti element. Primeri:
  A = {n; (n ∈ ) ∧ (n ≤ 6)} = {1, 2, 3, 4, 5, 6}

Pogosto srečamo tudi zapis s formulo. Pred podpičjem navedemo formulo, po kateri izračunamo elemente množice. Primeri:
  B = {2k; k ∈ } = {2, 4, 6, 8, 10, 12, ...}
  C = {2k + 1; k ∈ } = {..., −3, −1, 1, 3, 5, ...}

Računanje z množicami

Presek množic A in B je množica sestavljena iz elementov, ki pripadajo množici A in množici B hkrati.
Presek množic A in B označimo A ∩ B.
  A ∩ B = {x; (x ∈ A) ∧ (x ∈ B)}

Množici, ki imata prazen presek (torej A ∩ B = Ø), imenujemo tuji ali disjunktni množici.

Unija množic A in B je množica sestavljena iz elementov, ki pripadajo množici A ali množici B (ali obema).
Unijo množic A in B označimo A ∪ B.
  A ∪ B = {x; (x ∈ A) ∨ (x ∈ B)}

Razlika množic A in B je množica sestavljena iz elementov, ki pripadajo množici A in hkrati ne pripadajo množici B.
Razliko množic A in B označimo A \ B ali tudi A − B.
  A \ B = {x; (x ∈ A) ∧ (x  B)}

Komplement množice A je množica sestavljena iz elementov, ki ne pripadajo množici A.
Označimo ga A' ali tudi A^C ali CA.
  A' = {x; x  A}

Komplement množice računamo vedno v okvirju neke širše množice, ki jo imenujemo univerzalna množica ali univerzum pogovora.
Označujemo jo z u. Torej velja:
  A' = u \ A

Moč množice

Moč množice je število elementov, ki jih množica vsebuje. Oznaka:
  m(A) = moč množice A

Primer:
  F = {−1, 0, 2, 3, 10}
  m(F) = 5

Moč unije množic lahko izračunamo po formuli:
  m(A ∪ B) = m(A) + m(B) − m(A ∩ B)

Podmnožice

Pravimo, da je množica A podmnožica množice B, če je vsak element množice A vsebovan tudi v množici B.
Oznaka: A ⊂ B (ali tudi A ⊆ B).
Podmnožica množice B je lahko tudi enaka množici B. Tiste podmnožice, ki niso enake množici B, imenujemo prave podmnožice množice B.

Množici A in B sta enaki, če vsebujeta iste elemente. To je res, samo če je množica A podmnožica množice B, hkrati pa je tudi množica B podmnožica množice A.
  A = B    ⇔    (A ⊂ B) ∧ (B ⊂ A)

Potenčna množica množice A je množica vseh podmnožic množice A.
  P A = {X; X ⊂ A}

Primer:
  A = {1, 2, 3}
  P A = { { }, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} }

Če ima množica A točno n elementov, potem ima 2ⁿ podmnožic, torej:
   m(A) = n    ⇒    m(P A) = 2ⁿ

Kartezični produkt množic

Urejen par je zapis sestavljen iz dveh elementov, pri čemer je pomembno, kateri element je na prvem in kateri na drugem mestu: (a, b). Elementa a in b, ki nastopata v zapisu urejenega para, imenujemo komponenti para. Urejeni par (a, b) ni enak urejenemu paru (b, a).

Kartezični produkt množic A in B je množica sestavljena iz urejenih parov, ki imajo prvo komponento iz množice A in drugo iz množice B.
Kartezični produkt množic A in B označimo A × B.
  A × B = {(a, b); (a ∈ A) ∧ (b ∈ B)}

Če ima množica A točno n elementov, množica B pa m elementov, potem ima kartezični produkt nm elementov.

Zgled:
  A = {1, 2, 3}
  B = {1, 2}
  A × B = {(1,1), (1,2), (2,1), (2,2), (3,1), (3,2)}

Elemente kartezičnega produkta lahko ponazorimo kot točke v koordinatnem sistemu:
  

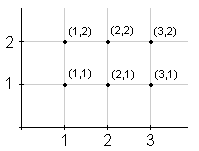
Kazalo poglavij

Izjave

Naravna in cela števila

Abecedno kazalo