| Kazalo poglavij | Neenačbe | Koordinatni sistem v prostoru | Abecedno kazalo |
Koordinatni sistem v ravnini
Koordinatni sistem v ravnini je sestavljen iz dveh med seboj pravokotnih premic, ki ju imenujemo abscisna os (vodoravna os, koordinatna os x) in ordinatna os (navpična os, koordinatna os y).Točkam na koordinatnih oseh priredimo realna števila. Pri tem praviloma uporabimo za obe osi isto dolžinsko enoto. Koordinatni sistem, ki ima na obeh oseh enako velike enote, imenujemo standardni koordinatni sistem. Veliko formul, ki jih bomo spoznali v nadaljevanju, velja samo, če so enote v vseh smereh (vodoravno, navpično, pa tudi poševno) enako velike. Zato le izjemoma uporabljamo nestandardni koordinatni sistem, ki ima na vodoravni osi drugačne enote kot na navpični. Več o tem lahko prebereš v dodatku.
Ravninski koordinatni sistem z dvema pravokotnima osema je odkril René Descartes - Renatus Cartesius. Zato koordinatni sistem take vrste imenujemo tudi kartezični ravninski koordinatni sistem, ravnino s koordinatnim sistemom pa imenujemo kartezična ravnina.
Koordinatni sistem uporabljamo zato, da poljubni točki T iz te ravnine določimo koordinati točke (zapis: T(x, y)). To sta števili, ki nam povesta, kje ležita projekciji točke T na koordinatni osi. Koordinati se imenujeta abscisa točke T (x koordinata točke T) in ordinata točke T (y koordinata točke T). Koordinati enolično natančno določata lego točke T v ravnini. Tako poljubni točki T iz ravnine priredimo točno en par realnih števil (x, y), poljubnemu paru realnih števil (x, y) pa priredimo točno eno točko T iz ravnine.
Zato pravimo, da je kartezična ravnina enaka kartezičnemu produktu
×
oziroma 2.
Zgled:
Točka A ima absciso enako 3 in ordinato enako 2. Torej A(3, 2):
Koordinatni osi razdelita ravnino na štiri dele, ki jih imenujemo kvadranti:
Premico, ki razpolavlja I. in III. kvadrant, imenujemo simetrala lihih kvadrantov; premico, ki razpolavlja II. in IV. kvadrant, pa imenujemo simetrala sodih kvadrantov.
Razdalja v koordinatah
Če poznamo koordinate točk A(x1, y1) in B(x2, y2), lahko izračunamo razdaljo |AB|.Pomagamo si s Pitagorovim izrekom in dobimo spodnjo formulo:
Ploščina trikotnika
Če poznamo koordinate točk A(x1, y1), B(x2, y2) in C(x3, y3), lahko izračunamo ploščino trikotnika ΔABC po formuli:S =
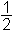| x1(y2 − y3) +
x2(y3 − y1) +
x3(y1 − y2) |Druga možna oblika zapisa te formule:
S =
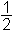| (x2 − x1)
(y3 − y1) −
(x3 − x1)
(y2 − y1) |V zgornji formuli (v obeh oblikah) nastopa absolutna vrednost, ker mora biti ploščina vedno nenegativno število. Če bi absolutno vrednost izpustili, bi bil rezultat lahko pozitiven ali negativen – glede na razporeditev oglišč v ravnini.
Oglišča trikotnika so lahko razporejena na dva načina:
Če si sledijo v obratni smeri urinih kazalcev, pravimo, da ima trikotnik pozitivno orientacijo in zapišemo: or = 1 (orientacija je enaka 1).
Če pa si sledijo v smeri urinih kazalcev, pravimo, da ima trikotnik negativno orientacijo in zapišemo: or = −1 (orientacija je enaka −1).
Produkt ploščine in orientacije imenujemo tudi orientirana ploščina trikotnika: S or. Izračunamo jo po formuli:
S or =
(
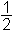x1(y2 − y3) +
x2(y3 − y1) +
x3(y1 − y2)
)oziroma (druga oblika formule):
S or =
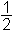( (x2 − x1)
(y3 − y1) −
(x3 − x1)
(y2 − y1) )To formulo pogosto zapišemo tudi v obliki determinante:
Determinanta je številska shema, sestavljena iz štirih števil, ki jih zapišemo v dve vrstici (po dve števili v vsako vrstico).
Vrednost determinante izračunamo po pravilu:
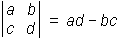
| Kazalo poglavij | Neenačbe | Koordinatni sistem v prostoru | Abecedno kazalo |