| Kazalo poglavij | Koordinatni sistem v ravnini | Funkcije | Abecedno kazalo |
Koordinatni sistem v prostoru
Koordinatni sistem v prostoru je sestavljen iz treh med seboj pravokotnih premic, ki jih imenujemo abscisna os (prva vodoravna os, koordinatna os x), ordinatna os (druga vodoravna os, koordinatna os y) in aplikatna os (navpična os, koordinatna os z).Točkam na koordinatnih oseh priredimo realna števila. Pri tem praviloma uporabimo za vse tri osi isto dolžinsko enoto. Koordinatni sistem, ki ima enako velike enote, imenujemo standardni koordinatni sistem. Veliko formul, ki jih bomo spoznali v nadaljevanju, velja samo, če so enote v vseh smereh (vodoravno, navpično, pa tudi poševno) enako velike. Zato le izjemoma uporabljamo nestandardni koordinatni sistem, ki ima različno velike enote. Več o tem lahko prebereš v dodatku
Prostorski koordinatni sistem s tremi pravokotnimi osmi je odkril René Descartes - Renatus Cartesius. Zato koordinatni sistem take vrste imenujemo tudi kartezični prostorski koordinatni sistem.
Koordinatni sistem uporabljamo zato, da poljubni točki T določimo koordinate točke (zapis: T(x, y, z)). To so števila, ki nam povedo, kje ležijo projekcije točke T na koordinatne osi. Koordinate se imenujejo abscisa točke T (x koordinata točke T), ordinata točke T (y koordinata točke T) in aplikata točke T (z koordinata točke T). Koordinate enolično natančno določajo lego točke T v prostoru. Tako poljubni točki T iz prostora priredimo točno eno trojico realnih števil (x, y, z), poljubni trojici realnih števil (x, y, z) pa priredimo točno eno točko T v prostoru.
Zato pravimo, da je prostor enak kartezičnemu produktu
 ×
×  ×
×  oziroma
oziroma  3.
3.
Prostorskega koordinatnega sistema ne moremo narisati v ravnini brez popačenja. Pri tem ponavadi narišemo eno od osi poševno - predstavljamo si, da ta os ponazarja smer »navznoter« (v papir, v tablo, v zaslon) oziroma »navzven« (ven iz papirja, iz table, iz zaslona).
Zgled:
Točka A ima absciso enako 4, ordinato enako 1 in aplikato enako 3. Torej A(4, 1, 3):

Razdalja v koordinatah
Če poznamo koordinate točk A(x1, y1, z1) in B(x2, y2, z2), lahko izračunamo razdaljo |AB| po naslednji formuli: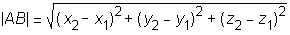
| Kazalo poglavij | Koordinatni sistem v ravnini | Funkcije | Abecedno kazalo |