Kazalo poglavij

Koordinatni sistem v prostoru

Lastnosti funkcij

Abecedno kazalo

Funkcije

Funkcija f :  A → B (funkcija iz množice A v množico B) je predpis (pravilo, postopek, preslikava, formula,..), ki danemu podatku x ∈ A priredi funkcijsko vrednost f (x) ∈ B.

Množica A je množica vseh podatkov, na katerih izvajamo funkcijo f; torej množica vseh podatkov, za katere je funkcija definirana. Imenujemo jo tudi definicijsko območje funkcije f. Oznaka: D_f
Množico vseh funkcijskih vrednosti, ki jih pri tem dobimo, imenujemo zaloga vrednosti funkcije f. Oznaka: Z _f
Zaloga vrednosti je lahko enaka množici B, lahko pa je tudi njena prava podmnožica.

Funkcija realne spremenljivke je funkcija, ki ima za podatke samo realna števila; torej: D _f ⊂ .
Realna funkcija je funkcija, ki ima za funkcijske vrednosti (tj. za rezultate) vedno samo realna števila; torej: Z _f ⊂ .

V matematiki najpogosteje srečujemo funkcije, ki imajo za podatke in za rezultate samo realna števila. Pravimo jim realne funkcije realne spremenljivke.
Dogovor: Zaradi krajšega izražanja bomo v nadaljevanju uporabljali izraz funkcija v ožjem pomenu:
  »funkcija« = »realna funkcija realne spremenljivke«

Podajanje funkcije

Funkcijo podamo s funkcijsko enačbo ali s funkcijskim predpisom. Oba vsebujeta ime funkcije (ponavadi f ), oznako neodvisne spremenljivke (ponavadi x) in formulo, po kateri izračunamo funkcijsko vrednost.

Zgled:
Funkcija f naj pomeni pravilo: »podatek kvadriraj in prištej 5.«
To funkcijo zapišemo s funkcijsko enačbo (beri: f od x je enako x² + 5):


... oziroma s funkcijskim predpisom (beri: f preslika x  v  x² + 5):

Ponazarjanje funkcije

Funkcijo ponazorimo s tabelo ali z grafom.

• Tabela funkcije podaja različne vrednosti spremenljivke x in ustrezne funkcijske vrednosti f (x).
  
  Zgled:
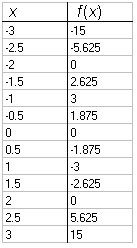
  Dana je funkcija f (x) = x³ − 4x.
  Zapišimo tabelo te funkcije na intervalu [−3, 3] s korakom 0.5:
    
  
  
• Graf funkcije je množica točk (x, y), za katere velja med koordinatama zveza y = f (x), torej:
     G_f = {(x, y); y = f (x)}
  
  Enačbo y = f (x) imenujemo tudi enačba grafa funkcije.
  
  Zgled:
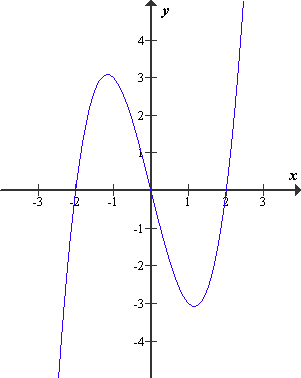
  Graf funkcije f (x) = x³ − 4x   (tj. množica točk, za katere velja enačba y = x³ − 4x):
  
    

Računanje s funkcijami

• Najpomembnejši računski postopek, ki ga računamo s funkcijami, je izračun funkcijske vrednosti pri danem podatku (vstavljanje podatka x v funkcijo).
  Zgled:
  Dana je funkcija f (x) = x² + 5x. Izračunajmo vrednost te funkcije pri x = 3. Dobimo:
    f (3) = 3² + 5 · 3 = 24
  
  
• Poleg tega lahko s funkcijami računamo štiri osnovne računske operacije:
  Funkciji f in g seštejemo, odštejemo, zmnožimo in delimo tako, da ustrezno računsko operacijo izračunamo za dani funkcijski vrednosti f (x) in g(x), torej:
  
    (f + g)(x) = f (x) + g(x)
    (f − g)(x) = f (x) − g(x)
    (f · g)(x) = f (x) · g(x)
    
  
  
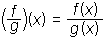
• Posebna računska operacija, ki jo računamo v množici funkcij, je kompozitum ali sestava funkcij. Kompozitum funkcij f in g označimo f ○ g in ga izračunamo po pravilu:
  
    (f ○ g)(x) = f (g(x))
  
  To pomeni, da podatek x najprej preslikamo s funkcijo g, tako da dobimo g(x), potem pa tako dobljeni rezultat preslikamo še s funkcijo f, tako da dobimo f (g(x)).
  Drugače povedano: kompozitum f ○ g dobimo tako, da v enačbo funkcije f namesto spremenljivke x vstavimo g(x).
  Rezultat kompozituma imenujemo tudi sestavljena funkcija.
  
  Zgled:
  Izračunajmo kompozitum naslednjih dveh funkcij.
    
  
  Iz zgornjega zgleda vidimo, da kompozitum f ○ g ni enak kompozitumu g ○ f (ne velja komutativnost).
  Izkaže pa se, da za kompozitum treh funkcij velja asociativnostni zakon:
    f ○ (g ○ h) = (f ○ g) ○ h
  
  V množici funkcij obstaja tudi funkcija, ki je nevtralni element za kompozitum. To je identična funkcija f_id(x) = x. Velja zakon o nevtralnem elementu:
    f ○ f_id = f_id ○ f = f
  
  Glej tudi: graf sestavljene funkcije.
  
  
• Inverzna funkcija je funkcija, ki deluje ravno obratno kot dana funkcija f. Če dana funkcija f preslika podatek x v rezultat y, potem inverzna funkcija preslika y nazaj v x. Izkaže se, da inverzna funkcija obstaja, samo če je dana funkcija f bijektivna funkcija f :  A → B.
  Inverzno funkcijo (če obstaja) označimo f ⁻¹ in to je funkcija f ⁻¹ :  B → A   (tj. f ⁻¹ je funkcija, ki preslikuje iz B v množico A).
  Inverzna funkcija f ⁻¹ deluje ravno obratno kot prvotna funkcija f, zato velja   (f ○ f ⁻¹)(x) = (f ⁻¹ ○ f )(x) = x
  
  Ker inverzna funkcija deluje ravno obratno kot prvotna funkcija f, se pri inverzni funkciji vloga podatka in rezultata zamenjata. Če je f (a) = b, potem je f ⁻¹(b) = a   (tj: če funkcija f preslika element a v element b, potem inverzna funkcija f ⁻¹ preslika element b v element a).
  
  Na tem pravilu je zasnovan tudi postopek določanja enačbe inverzne funkcije:
  Najprej enačbo prvotne funkcije zapišemo v obliki y = f (x).
  Potem v tej enačbi zamenjamo črki x in y (zamenjamo vlogo podatka in rezultata).
  Potem iz dobljene enačbe izrazimo y in tako dobimo enačbo inverzne funkcije.
  
  Zgled:
  Poiščimo inverz funkcije f (x) = 2x + 5. Najprej zapišimo:
    f :   y = 2x + 5
  Zamenjamo x in y in izrazimo y:
    f ⁻¹:   x = 2y + 5
          −2y = −x + 5
            y =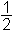 x − 
  
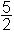
  Torej je enačba inverzne funkcije:
    f ⁻¹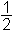(x) = x −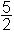 
  
  Kot smo že zapisali, inverz funkcije f obstaja, samo če je funkcija f bijektivna. Kaj pa sicer? Pogosto si pomagamo tako, da funkcijo f omejimo (zožimo) na manjše definicijsko območje in s tem dosežemo, da je zožena funkcija f :  A → B bijektivna.
  Potem obstaja inverz f ⁻¹ :  B → A. Tak inverz včasih imenujemo tudi delni inverz.
  
  Zgled:
  Funkcija f (x) = x² ni bijektivna (točneje: ni bijektivna funkcija  → ).
  Če pa jo zožimo na nenegativna števila, hitro ugotovimo, da je f bijektivna funkcija ₀⁺→ ₀⁺.
  V smislu te zožitve obstaja tudi inverzna funkcija f ⁻¹ :  ₀⁺→ ₀⁺, ki ima enačbo f ⁻¹(x) = .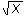
  
  Glej tudi: graf inverzne funkcije.
  
  

Kazalo poglavij

Koordinatni sistem v prostoru

Lastnosti funkcij

Abecedno kazalo