Risanje grafov funkcij

Premiki in raztegi

y = f (x) + q . . . P_y q
Število q, ki ga prištejemo funkciji, pomeni premik grafa funkcije v smeri osi y za q.
Pri tem se y koordinata vsake točke na grafu poveča za q (in x koordinata ostane nespremenjena).

Zgled:
y = a f (x)     . . .    R_y a
Število a s katerim pomnožimo funkcijo, pomeni razteg grafa funkcije v smeri osi y za faktor a.
Pri tem se y koordinata vsake točke na grafu pomnoži s številom a (in x koordinata ostane nespremenjena).

Zgled:


Razteg v smeri osi y za faktor −1 pomeni zrcaljenje grafa funkcije čez abscisno os.
y = f (x − p) . . . P_x p
Število p, ki ga odštejemo od neodvisne spremenljivke x, pomeni premik grafa funkcije v smeri osi x za p.
Pri tem se x koordinata vsake točke na grafu poveča za p (in y koordinata ostane nespremenjena).

Zgled:
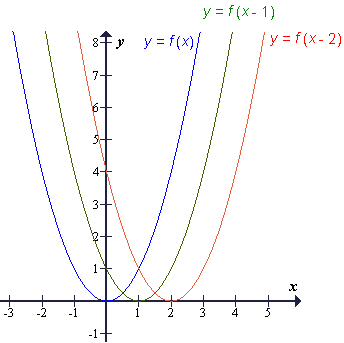
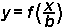. . . R_x b

Število b s katerim delimo neodvisno spremenljivko x, pomeni razteg grafa funkcije v smeri osi x za faktor b.
Pri tem se x koordinata vsake točke na grafu pomnoži s številom b (in y koordinata ostane nespremenjena).
Razteg v smeri osi x za faktor −1 pomeni zrcaljenje grafa funkcije čez ordinatno os.

Zgled:
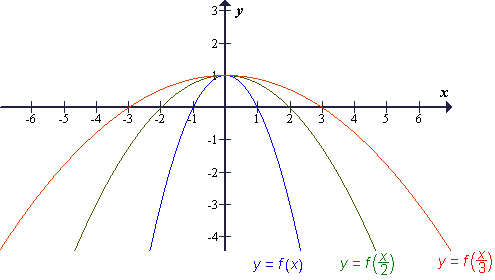
Premik grafa za vektor (p, q) pomeni, da hkrati izvedemo premik v smeri osi x za p in premik v smeri osi y za q.

Absolutna vrednost pri grafih

y = |f (x)|
Graf y = |f (x)| dobimo iz grafa funkcije y = f (x) tako, da
(1) ohranimo nespremenjene vse tiste dele grafa, kjer je vrednost funkcije f pozitivna ali enaka 0,
(2) tiste dele, kjer je funkcija f negativna, pa prezrcalimo čez abscisno os.
y = f (|x|)
Graf y = f (|x|) dobimo iz grafa funkcije y = f (x) tako, da
(1) ohranimo nespremenjen tisti del grafa, kjer je x pozitiven ali enak 0 (desni del grafa),
(2) potem pa desni del grafa še prezrcalimo čez ordinatno os (na levo stran).
y = |f (|x|)|
Graf y = |f (|x|)| dobimo tako, da izvedemo oba zgoraj opisana postopka (vseeno po kakšnem vrstnem redu).

Zgled:
Podan je graf funkcije y = f (x)
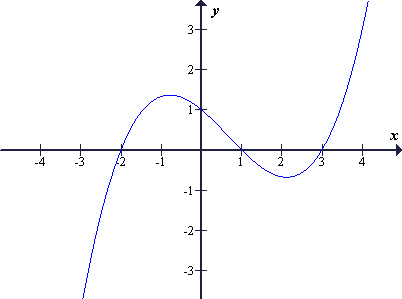
Graf - zgled

Narišimo grafe:
y = |f (x)|
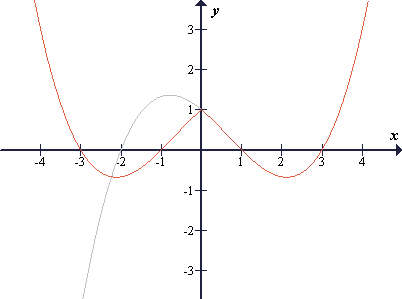
Graf z absolutno vrednostjo

y = f (|x|)
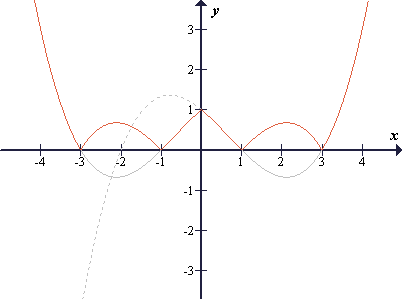
Graf z absolutno vrednostjo

y = |f (|x|)|
Graf z absolutno vrednostjo

Graf sestavljene funkcije

Graf sestavljene funkcije y = f (g(x)) (tj. graf kompozituma f ○ g) lahko narišemo v dveh korakih:
(1) najprej narišemo graf prve (notranje) funkcije y₁ = g(x),
(2) Potem pa y koordinato vsake točke na tem grafu preslikamo še s funkcijo f, torej: y = f (y₁) (koordinata x pa ostane nespremenjena).

Zgled:
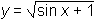Graf funkcije koren(sin x + 1)

narišemo tako, da
(1) najprej narišemo graf y = sin x + 1,
(2) potem pa y koordinato vsake točke na grafu korenimo.
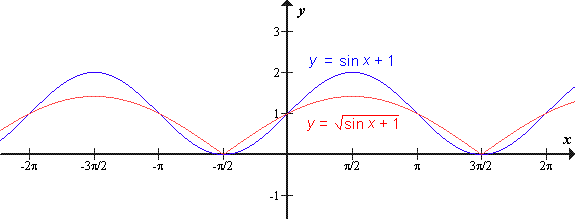
Graf sestavljene funkcije

Graf inverzne funkcije

Graf inverzne funkcije y = f ⁻¹(x) lahko narišemo tako, da prezrcalimo graf osnove funkcije y = f (x) čez simetralo lihih kvadrantov.

Zgled:
Narišimo graf funkcije f (x) = x³ − 1,
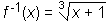
potem pa še graf inverzne funkcije 3koren(x+1)