Izjave

Izjava je vsak smiseln povedni stavek. V matematiki izjave označujemo s črkami, npr.:
  A: Zemlja kroži okoli Sonca.
  B: Število 5 je praštevilo.
  C: Vsota števil 1 in 2 je enaka 17.

Izjava je lahko pravilna ali nepravilna - temu pravimo vrednost izjave. Med zgornjimi tremi izjavami sta prvi dve pravilni, tretja pa je nepravilna. To označimo:
  A ~ p
  B ~ p
  C ~ n

Računanje z izjavami

Konjunkcija izjav A in B je izjava, ki je pravilna, samo kadar sta pravilni obe delni izjavi (A in B hkrati).
Konjunkcijo izjav označimo:
  A ∧ B        (beri: A in B)

Disjunkcija izjav A in B je izjava, ki je pravilna, samo kadar je pravilna vsaj ena od delnih izjav (ali A ali B ali obe hkrati).
Disjunkcijo izjav označimo:
  A ∨ B        (beri: A ali B)

Negacija izjave A je izjava, ki je pravilna, samo kadar je izjava A nepravilna.
Negacijo izjave A označimo:
  ¬ A        (beri: ne A)

Implikacija izjav A in B je izjava, ki je pravilna, samo kadar je pravilno sklepanje, da iz A sledi B (torej kadar je izjava A nepravilna ali pa izjava B pravilna).
Implikacijo izjav označimo:
  A ⇒ B        (beri: iz A sledi B oziroma: če A potem B)

Ekvivalenca izjav A in B je izjava, ki je pravilna, samo kadar sta izjavi A in B po vrednosti enaki (obe hkrati pravilni ali obe hkrati napačni).
Ekvivalenco izjav označimo:
  A ⇔ B        (beri: A ekvivalentno B oziroma: A če in samo če B)

Sestavljene izjave

Iz osnovnih izjav A, B, C,... lahko z zgoraj navedenimi računskimi operacijami sestavljamo sestavljene izjave. Pravilnost take sestavljene izjave preverimo s pravilnostno tabelo.
Primer:
  

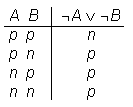
Sestavljeno izjavo, ki je vedno pravilna, imenujemo logično pravilna izjava ali tavtologija.
Taka je npr. izjava A ∨ ¬A.

Če imata dve izjavi v istih okoliščinah vedno enako vrednost (sta vedno obe pravilni ali obe napačni), pravimo, da sta enakovredni. Enakovredni sestavljeni izjavi imata enako pravilnostno tabelo. Če sta izjavi X in Y enakovredni, potem je sestavljena izjava X ⇔ Y tavtologija.
Zgled:   ¬ (A ∧ B)   in   ¬A ∨ ¬B   sta enakovredni izjavi.

Kvantifikatorja

Kvantifikatorja sta znaka ∀ in ∃, ki nam povesta, za koliko elementov velja določena izjava.

Kvantifikator ∀ (beri: vsak) pomeni, da izjava velja za vsak element dane množice.
Primera:
  ∀x:   x + 1 > x    (Za vsak x velja, da je x + 1 več od x.)
  ∀a ∈ :   a² ≥ 0    (Za vsako realno število a velja, da je a² večji ali enak 0.)

Kvantifikator ∃ (beri: obstaja oziroma eksistira) pomeni, da obstaja v dani množici vsaj en element, za katerega je izjava pravilna.
Primer:
  ∃n ∈ :   n = n²    (Obstaja vsaj eno naravno število n, ki je enako svojemu kvadratu.)

Pomen izjav v matematiki

Izjave so osnova vsake matematične teorije. Z izjavami opisujemo lastnosti matematičnih objektov. Ločimo nekaj različnih vrst izjav:

Aksiomi so najpreprostejše izjave, ki so očitno pravilne in zato njihove pravilnosti ni treba dokazovati.

Izreki ali teoremi so izjave, ki so pravilne, vendar pa njihova pravilnost ni očitna. Pravilnost izreka (teorema) moramo potrditi z dokazom, ki temelji na aksiomih in na preprostejših že prej dokazanih izrekih.

Definicije so izjave, s katerimi uvajamo nove pojme. Najpreprostejših pojmov v matematiki ne opisujemo z definicijami (to so pojmi kot npr.: število, premica ipd.); vsak nadaljni pojem pa moramo definirati, zato da se nedvoumno ve, o čem govorimo.

Kazalo poglavij

Uvod

Množice

Abecedno kazalo