Kazalo poglavij

Kompleksna števila

Enačbe in sistemi

Abecedno kazalo

Matematični izrazi

Matematični izraz je zapis sestavljen iz:
- števil,
- spremenljivk, ki predstavljajo števila in jih označujemo s črkami,
- računskih operacij in funkcij, ki jih povezujejo,
- oklepajev, ki določajo vrstni red računanja.

Če v izraz namesto spremenljivk vstavimo konkretna števila in izračunamo rezultat, dobimo vrednost izraza (pri dani izbiri spremenljivk).

Dva matematična izraza sta enakovredna, če imata pri katerikoli izbiri spremenljivk vedno enako vrednost.

Izraz poimenujemo glede na glavno računsko operacijo (ali funkcijo), ki v tem izrazu nastopa. Glavna računska operacija (ali funkcija) je tista, ki jo izračunamo nazadnje.
Primeri:
Izraz   3a + ac − 5c²   ima obliko vsote (je vsota členov 3a,  ac in −5c²).
Izraz   (x + y)(2x − 3)   ima obliko produkta (je produkt faktorjev (x + y) in (2x − 3)).
Izraz 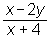    ima obliko količnika oz. ulomka (je količnik izrazov x − 2y in x + 4).

Razčlenjevanje izrazov

Preoblikovanje izraza v obliko vsote členov imenujemo razčlenjevanje. Pri razčlenjevanju izrazov uporabljamo zlasti naslednje postopke oziroma formule:

• Distributivnost (zakon o razčlenjevanju):
  a (b + c) = a b + a c
  
  
• Kvadrat dvočlenika (kvadrat vsote):
  (a + b)² = a² + 2ab + b²
  
  
• Kub dvočlenika (kub vsote):
  (a + b)³ = a³ + 3a²b + 3ab² + b³
  
  
• Binomska formula (n-ta potenca vsote za poljuben n ∈ ):
  
  
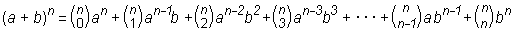
  (Opomba: Za razlago binomskega simbola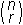 glej poglavje Kombinatorika.)
  
  

Razcepljanje izrazov

Preoblikovanje izraza v obliko produkta faktorjev imenujemo razcepljanje, razstavljanje ali faktorizacija. Pri razcepljanju izrazov uporabljamo zlasti naslednje postopke oziroma formule:

• Izpostavljanje (če distributivnostni zakon uporabimo v tej smeri, ga imenujemo tudi zakon o izpostavljanju):
  a b + a c = a (b + c)
  
  
• Razlika kvadratov:
  a² − b² = (a − b)(a + b)
  
  
• Vsota kvadratov je v nerazcepna, v 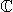pa jo lahko razcepimo po pravilu:
  a² + b² = (a − bi )(a + bi )
  
  
• Razlika kubov:
  a³ − b³ = (a − b)(a² + ab + b²)    (opomba: v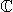 se da razcepiti tudi izraz v drugem oklepaju)
  
  
• Vsota kubov:
  a³ + b³ = (a + b)(a² − ab + b²)    (opomba: v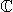 se da razcepiti tudi izraz v drugem oklepaju)
  
  
• Razlika n-tih potenc (n ∈ ):
  aⁿ − bⁿ = (a − b)(aⁿ⁻¹ + aⁿ⁻²b + aⁿ⁻³b² + ∙ ∙ ∙ + bⁿ⁻¹)
  
  
• Vsota n-tih potenc (n ∈ ) je v realnem razcepna, samo če je je n liho število:
  aⁿ + bⁿ = (a + b)(aⁿ⁻¹ − aⁿ⁻²b + aⁿ⁻³b² − ∙ ∙ ∙ + bⁿ⁻¹)
  
  
• Razcep kvadratnega tričlenika po Viètovem pravilu:
  x² + (a+b)x + ab = (x + a)(x + b)

Kazalo poglavij

Kompleksna števila

Enačbe in sistemi

Abecedno kazalo