Kompleksna števila

V množici realnih števil ne moremo rešiti enačbe: x² = −1. Če je x pozitiven ali enak 0, rezultat kvadriranja ne more biti negativen. Če je x negativen, pa predznak pri kvadriranju odpade in rezultat kvadriranja spet ne more biti negativen. Tako vidimo, da leva stran ne more biti enaka desni niti za pozitiven x niti za negativen x niti za x = 0.
Če dopustimo možnost, da rešitev zgornje enačbe vseeno obstaja, ta rešitev nikakor ne more biti niti pozitivna niti negativna niti enaka 0. Odločimo se, da rešitev zgornje enačbe označimo z oznako i. To število imenujmo imaginarna enota. Ker število i ne more biti niti pozitivno niti negativno niti enako 0, vidimo, da i sploh ne more biti realno število.

Očitno ima zgornja enačba še eno rešitev, namreč −i. Tudi število −i ne more biti realno število.
Če nadaljujemo z računanjem, dobimo še več števil, ki niso elementi množice

, npr.: i + i = 2i, 2i + 3i = 5i ...
Vsa dobljena števila imajo obliko bi (za b ∈

). Imenujemo jih imaginarna števila. Poskusimo tako število sešteti z običajnim realnim številom a. Dobljeni rezultat je število sestavljeno iz dveh delov: realnega in imaginarnega. Zapišemo ga kot vsoto: a + bi. Taka števila imenujemo kompleksna števila.

Množico kompleksnih števil označimo s

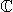. Torej je:

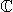= {a + bi; a, b ∈

}

Poljubno kompleksno število z lahko torej zapišemo v obliki: z = a + bi (a, b ∈

).
Realno število a, ki nastopa v tem zapisu, imenujemo realna komponenta števila z in to zapišemo: Re z = a.
Realno število b, ki nastopa v tem zapisu, imenujemo imaginarna komponenta števila z in to zapišemo: Im z = b.

Če je imaginarna komponenta števila z enaka 0, ima število z samo realno komponento. V tem primeru je število z realno število. To pomeni, da realna števila razumemo kot podmnožico množice kompleksnih števil:

⊂

Geometrijska upodobitev kompleksnih števil

Realna števila smo upodobili na realni osi. Ker realna števila realno os popolnoma pokrijejo, je jasno, da kompleksnih števil ne moremo upodobiti na številski premici.
Za upodobitev kompleksnih števil potrebujemo ravnino z ustreznim koordinatnim sistemom. Na vodoravno os (ki predstavlja realno os) nanašamo realna števila, na navpično os (ki jo imenujemo tudi imaginarna os) pa nanašamo imaginarna števila.
Kompleksno število a + bi upodobimo s točko, ki ima koordinati T(a, b).

Kompleksna ravnina

Upodobitev kompleksnih števil s točkami ravnine je povratno enolična, torej: vsakemu kompleksnemu številu pripada točno ena točka ravnine in vsaki točki ravnine pripada točno eno kompleksno število.
Ravnina je v tem smislu enakovredna množici kompleksnih števil, zato tako ravnino imenujemo tudi kompleksna ravnina (oziroma po odkritelju tudi Gaußova ravnina).

Včasih uporabljamo tudi geometrijsko upodobitev kompleksnih števil z ravninskimi vektorji. Pri tem kompleksno število a + bi upodobimo kot vektor, ki poteka od izhodišča do točke T(a, b) (tj. krajevni vektor točke T(a, b)).

Predstavitev z vektorji

Računanje s kompleksnimi števili

Dve kompleksni števili seštejemo (oziroma odštejemo) tako, da med sabo seštejemo (odštejemo) obe realni komponenti in potem še obe imaginarni komponenti. Torej:
(a + bi) + (c + di) = (a+c) + (b+d)i
(a + bi) − (c + di) = (a−c) + (b−d)i

Seštevanje kompleksnih števil geometrijsko ustreza seštevanju ustreznih krajevnih vektorjev: Če seštejemo krajevna vektorja števil z in w, dobimo ravno krajevni vektor vsote z + w.
Dve kompleksni števili zmnožimo tako, da upoštevamo distributivnostni zakon (pomnožimo vsak člen prvega oklepaja z vsakim členom drugega oklepaja) in pravilo i ² = −1.

Zgled: (2 + 3i)(4 + 5i) = 8 + 10i + 12i + 15i ² = 8 + 22i − 15 = −7 + 22i

Splošno:
(a + bi)(c + di) = (ac − bd) + (ad+bc)i
Pri deljenju kompleksnih števil si pomagamo tako, da deljenje zapišemo v obliki ulomka in potem števec in imenovalec pomnožimo s konjugirano vrednostjo imenovalca.
Zgled: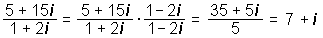
Konjugirano vrednost kompleksnega števila a + bi dobimo tako, da spremenimo predznak pri imaginarnem delu.
Konjugirana vrednost števila z = a + bi je torej število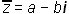
Za konjugiranje veljajo naslednje zakonitosti:

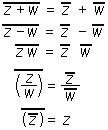
Absolutna vrednost kompleksnega števila

Absolutna vrednost kompleksnega števila z je oddaljenost točke, ki predstavlja to število v kompleksni ravnini, od izhodišča koordinatnega sistema. To je hkrati tudi dolžina krajevnega vektorja, ki ponazarja to število v kompleksni ravnini.

Absolutno vrednost kompleksnega števila z = a + bi izračunamo po naslednjih dveh formulah:
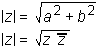
Absolutna vrednost

Za absolutno vrednost kompleksnega števila veljata naslednji dve lastnosti:
|z w| = |z| |w|
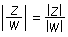
Lastnosti absolutne vrednosti