Kazalo poglavij

Geometrijska telesa

Zaporedja

Abecedno kazalo

Vektorji

Usmerjena daljica (oziroma orientirana daljica) je daljica, ki ji priredimo usmeritev (orientacijo). To naredimo tako, da se odločimo, katero od krajišč je začetna točka in katero končna točka te daljice.
Usmerjeno daljico z začetno točko A in končno točko B označimo .

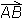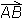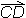Vektorji so matematične količine, ki jih ponazarjamo z usmerjenimi daljicami. Pri tem usmerjeni daljici in predstavljata isti vektor, če izpolnjujeta naslednje tri pogoje:
- sta enako dolgi,
- sta vzporedni,
- sta enako usmerjeni (enako orientirani).
  

Dani vektor lahko ponazorimo z usmerjeno daljico, ki se začne v poljubni točki - pravimo tudi, da vektor vzporedno premaknemo v dano začetno točko.

V množico vseh vektorjev dodamo kot poseben element še vektor nič (oznaka 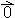), ki ga ponazormimo s točko. To je edini vektor, ki ima dolžino enako 0 in nima določene smeri.

Seštevanje vektorjev

Vektorje seštevamo po pravilu: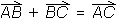   

To pomeni, da vektorja in seštejemo tako, da ju najprej vzporedno premaknemo v takšno lego, da je končna točka prvega vektorja hkrati začetna točka drugega, nato pa narišemo vsoto  + , ki poteka od začetne točke prvega do končne točke drugega vektorja.




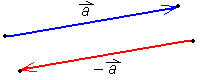
Nasprotni vektor vektorja je vektor, ki je enako dolg in vzporeden vektorju , ima pa nasprotno orientacijo (usmeritev).
Nasprotni vektor označimo   −.


Za seštevanje vektorjev veljajo naslednji zakoni (primerjaj z zakoni za seštevanje števil):


Odštevanje vektorjev definiramo kot prištevanje nasprotnega vektorja, torej:
   −  =  + (−)

Množenje vektorja s številom

Pri množenju vektorja z realnim številnom n, dobimo za rezultat vektor n, ki je določen z naslednjimi lastnostmi:
- vektor n je vzporeden vektorju ,
- dolžina vektorja n je |n|-krat tolikšna kot dolžina vektorja ,
- če je število n pozitivno, je vektor n enako orientiran kot ;
  če je število n negativno, pa je vektor n orientiran nasprotno kot .

(Opomba: če je n = 0, je rezultat množenja vektor 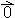. Po dogovoru velja, da je ta vektor vzporeden s poljubnim drugim vektorjem.)



Lastnosti množenja vektorja s številom
Za poljubna vektorja in in za poljubni realni števili m in n velja:
  n( + ) = n + n
  (n + m) = n + m

Linearne kombinacije in odvisnost

Linearna kombinacija vektorjev je vsak izraz, ki se ga da zapisati kot vsoto vektorjev pomnoženih s poljubnimi realnimi števili.
Zgledi linearnih kombinacij:
  

Dani vektorji so med sabo linearno odvisni, če se da enega izmed njih zapisati kot linearno kombinacijo ostalih.
Če to ni mogoče, pravimo, da so dani vektorji linearno neodvisni.

• Dva vektorja sta linearno odvisna, če in samo če sta vzporedna. V tem primeru lahko enega od njiju izrazimo z drugim, npr.:  = n.
  Če vzporedna vektorja prenesemo v skupno začetno točko, vidimo, da ležita na isti premici. Zato pravimo tudi, da sta kolinearna.
  Za dva vektorja torej velja:
     in sta odvisna   ⇔   in sta vzporedna   ⇔   in sta kolinearna.
  
  
• Trije vekorji so linearno odvisni, če in samo če so koplanarni. Vektorji so koplanarni, če ležijo v isti ravnini, kadar jih narišemo iz skupne začetne točke.
  
  
• Poljubni štirje vektorji (v običajnem prostoru) so vedno linearno odvisni.
  
  

Baza je skupina vektorjev, ki ima naslednji dve lastnosti:
- bazni vektorji so med sabo neodvisni,
- vsak drug vektor (v okviru dane množice) lahko izrazimo kot linearno kombinacijo baznih vektorjev.

Število baznih vektorjev imenujemo dimenzija ali razsežnost.

• Baza premice je poljuben neničelen vektor. Dimenzija premice je enaka 1. (Premica je enorazsežna.)
  
  
• Bazo ravnine sestavljata poljubna neničelna nevzporedna vektorja. Dimenzija ravnine je torej enaka 2. (Ravnina je dvorazsežna).
  
  
• Bazo prostora sestavljajo trije neničelni vektorji, ki ne ležijo v isti ravnini. Dimenzija prostora je enaka 3. (Prostor je trirazsežen.)
  
  

Bazo uporabljamo zato, da z baznimi vektorji izrazimo ostale vektorje (v okviru dane množice).
Zgled:
Če v ravnini izberemo bazo sestavljeno iz dveh neničelnih nevzporednih vektorjev in , potem lahko poljuben vektor iz te ravnine zapišemo kot linearno kombinacijo baznih vektorjev:  = n + m

Temu zapisu pravimo tudi razvoj vektorja po bazi , . Števili n in m, ki nastopata v razvoju, imenujemo komponenti.

Koordinate vektorjev

Kadar vektorje rišemo v koordinatnem sistemu (v ravnini ali v prostoru), lahko za začetno točko vektorja izberemo izhodišče koordinatnega sistema. Takemu vektorju pravimo krajevni vektor:
Krajevni vektor točke A je vektor, ki se začne v izhodišču koordinatnega sistema in konča v točki A. Označimo ga 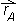in definiramo:
Krajevni vektor točke A ima iste koordinate kot točka A.

Bazo ravnine sestavljata poljubna neničelna nevzporedna vektorja. Če je v ravnini podan pravokotni koordinatni sistem, ponavadi izberemo za bazo ravnine vektorja 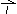in , ki sta določena z naslednjimi lastnostmi:
- imata dolžino enako 1 (sta enotska),
- sta pravokotna,
- vektor 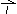ima smer osi x, vektor pa ima smer osi y.
To bazo imenujemo standardna ortonormirana baza ravnine.

V prostoru moramo dodati še tretji bazni vektor 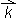, ki je tudi enotski in ima smer osi z. Baza 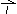, , 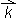je standardna ortonormirana baza prostora.

Koordinate poljubnega vektorja so enake kot komponente pri razvoju tega vektorja po standardni ortonormirani bazi.
  

Računanje s koordinatami vektorjev
Vektorje podane s koordinatami lahko seštevamo in množimo s števili:
   +  = (a₁ + b₁, a₂ + b₂, a₃ + b₃)
  n = (na₁, na₂, na₃)

Dolžino vektorja izračunamo po pravilu: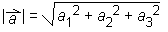
  

Koordinate vektorja s poljubno začetno točko A in končno točko B dobimo po pravilu:
  

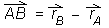
Če je točka S razpolovišče daljice AB, lahko krajevni vektor točke S izračunamo po pravilu:
  

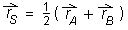
Skalarni produkt

Skalarni produkt je računska operacija, ki ima za podatka vektorja in , za rezultat pa realno število (skalar), ki ga izračunamo po pravilu:
    = || || cos φ
Pri tem φ označuje kot, ki ga oklepata vektorja, če ju narišemo iz skupne začetne točke.

Če sta vektorja podana s koordinatami, lahko skalarni produkt izračunamo po pravilu:
    = a₁b₁ + a₂b₂ + a₃b₃

Lastnosti skalarnega produkta
Za poljubne vektorje , in in za poljubno realno število n velja:
    =  
   ( + ) =   +  
  (n) = (n) = n()
    = ||²

Skalarni produkt lahko izrazimo tudi s projekcijo enega vektorja na drugega:
  

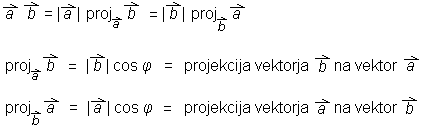
Skalarni produkt pogosto uporabljamo za računanje kota med vektorjema:
  

  

Vektorski produkt*

Vektorski produkt je računska operacija, ki ima za podatka vektorja in , za rezultat pa vektor, ki ga označimo  ×  in je določen z naslednjimi pravili:

• Vektor  ×  je pravokoten na vektor in na vektor .
• Dolžina vektorja  ×  je enaka ploščini paralelograma, ki ga določata vektorja in , če ju narišemo iz skupne začetne točke.
• Orientacija vektorja  ×  je določena s pravilom desne roke (če spodnji del desne roke zasukamo z dlanjo naprej po krajši poti od vektorja do vektorja , potem palec kaže v smeri vektorskega produkta).

Če sta vektorja podana s koordinatami, lahko vektorski produkt izračunamo po pravilu:
   ×  = (a₂b₃ − a₃b₂, a₃b₁ − a₁b₃, a₁b₂ − a₂b₁)

Lastnosti vektorskega produkta
Za poljubne vektorje , in in za poljubno realno število n velja:
   ×  = −  × 
   × ( + ) =  ×  +  × 
  ( + ) ×  =  ×  +  × 
  (n) ×  =  × (n) = n( × )
   ×  =

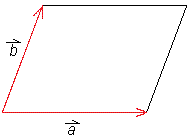
Vektorski produkt uporabljamo za računanje ploščine paralelograma:
  S = | × |

  

Vektorski in skalarni produkt skupaj lahko uporabimo za računanje prostornine paralelepipeda:
  V = |( × ) |

  

---

*Opomba: Po učnem načrtu za gimnazije sodi poglavje Vektorski produkt med izbirne vsebine. Obravnavamo ga samo v razredih, ki kažejo poseben matematični interes.

Kazalo poglavij

Geometrijska telesa

Zaporedja

Abecedno kazalo