Geometrijska telesa

Geometrijsko telo je strnjen del prostora, omejen s sklenjeno ploskvijo. Če je mejna ploskev telesa sestavljena iz samih večkotnikov, pravimo takemu telesu polieder. Če te večkotnike prenesemo v ravnino, dobimo ravninsko mrežo poliedra.

Površina in prostornina

Površina poliedra je vsota ploščin vseh njegovih mejnih ploskev.
(Na splošno je površina telesa vsota površin vseh njegovih mejnih ploskev - tudi če te ploskve niso ravne.)
Površino označimo s črko P.

Prostornina ali volumen telesa nam pove, koliko prostorninskih enot (enotskih kockic) potrebujemo, da dano telo povsem zapolnimo. Če se postopek zapolnjevanja ne izide, nadaljujemo z manjšimi enotami (tisočinami, milijoninami,...).
Volumen označujemo s črko V.

Prizme

Prizma je polieder omejen z dvema osnovnima ploskvama in plaščem. Osnovni ploskvi sta skladna, vzporedna večkotnika. Plašč je sestavljen iz paralelogramov, ki povezujejo obe osnovni ploskvi.

Robovi obeh osnovnih ploskev prizme so osnovni robovi, ostalim robovom pravimo stranski robovi.
Višina prizme je razdalja med obema osnovnima ploskvama.

Prizma, ki ima za osnovno ploskev n-kotnik, je n-strana prizma.
Pokončna prizma ima vse stranske robove pravokotne na osnovno ploskev. Dolžina stranskega roba je v tem primeru enaka višini. Prizma, ki ni pokončna, je poševna.
Enakoroba prizma ima vse robove enako dolge.
Pravilna n-strana prizma ima za osnovno ploskev pravilni n-kotnik in je pokončna.

Zgled:
Prizma

Prostornina in površina prizme
Če označimo:
O = ploščina osnovne ploskve,
v = višina prizme,
pl = plašč (vsota ploščin vseh paralelogramov, ki sestavljajo plašč),
potem veljata za prostornino in površino prizme formuli:

  V = O v
  P = 2O + pl

Za pokončne prizme velja poleg tega še formula:
  pl = ov      (o = obseg osnovne ploskve)

Piramide

Piramida je polieder omejen z osnovno ploskvijo in plaščem. Osnovna ploskev je poljuben večkotnik, plašč pa je sestavljen iz trikotnikov, ki povezujejo osnovno ploskev s točko, ki jo imenujemo vrh piramide.

Robovi osnovne ploskve so osnovni robovi piramide, ostali robovi so stranski robovi.
Višina piramide je oddaljenost vrha od osnovne ploskve. Višina kot daljica poteka od vrha do ravnine osnovne ploskve in je na to ravnino pravokotna.

Piramida, ki ima za osnovno ploskev n-kotnik, je n-strana piramida.
Enakoroba piramida ima vse robove enako dolge.
Pravilna n-strana piramida ima za osnovno ploskev pravilni n-kotnik in ima vse stranske robove enako dolge.

(Opomba: Pogosto srečamo tudi pojem pokončna piramida, vendar ta pojem ni povsod enako definiran. Ponavadi velja, da je piramida pokončna, če leži spodnje krajišče višine v središču osnovne ploskve. Obstajajo pa različni možni odgovori na vprašanje, kaj je središče osnovne ploskve. Izberemo lahko npr.:
(a) središče očrtane krožnice - ne obstaja vedno, če pa obstaja, so vsi stranski robovi enako dolgi, a piramida lahko stoji "postrani";
(b) težišče - obstaja vedno, a včasih ni "lepa" točka;
(c) središče včrtane krožnice, ipd.
Piramida, ki ni pokončna, je poševna.)

Zgled:

Prostornina in površina piramide
Če označimo:
O = ploščina osnovne ploskve,
v = višina piramide,
pl = plašč (vsota ploščin vseh trikotnikov, ki sestavljajo plašč),
potem veljata za prostornino in površino piramide formuli:
V = 1/3

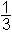O v

P = O + pl

Kot vidimo iz formule za prostornino, velja tretjinsko pravilo:
Prostornina piramide je tretjina prostornine prizme z enako osnovno ploskvijo in enako višino.

Valj, stožec in krogla

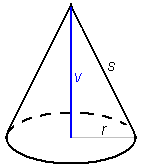
	Pokončni krožni valj V = π r ² v P = 2 π r ² + 2 π r v
	Pokončni stožec 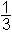V = π r ² v P = π r ² + π r s
	Krogla V = 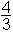π r ³ P = 4 π r ²