Potenčna funkcija

Potence s celimi eksponenti

Potenco aⁿ definiramo za eksponent n ∈

kot produkt n-tih faktorjev, ki so vsi enaki a (a je poljubno realno ali tudi kompleksno število):
aⁿ = a · a · a · · · a (n faktorjev)

Za ostale celoštevilske eksponente definiramo potenco z naslednjima zvezama:
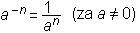
a⁰ = 1, Potenca z negativnim eksponentom

Potence z necelimi eksponenti definiramo s pomočjo korenov.

Za potence veljajo naslednja računska pravila:

aⁿ a^m = a^n+m
an/am

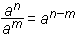
  (aⁿ)^m = a^nm
  (ab)ⁿ = aⁿ bⁿ
   an/bn

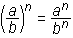
Grafi in lastnosti potenčnih funkcij

Potenčna funkcija je funkcija, ki jo lahko zapišemo z enačbo oblike f (x) = xⁿ (za n ∈

).

Funkciji, ki ju dobimo za n = 0 in n = 1, sta pravzaprav linearni funkciji f (x) = 1 in f (x) = x, zato ju ne uvrščamo med prave potenčne funkcije.
Ostale potenčne funkcije lahko razdelimo v naslednje štiri skupine:

Potenčne funkcije z lihim pozitivnim eksponentom (večjim od 1):

Vsaka funkcija iz te skupine ima naslednje lastnosti:
- D_f = ,
- Z_f = ,
- je liha,
- v okolici točke T(0, 0) je graf vodoraven (ima vodoravni prevoj),
- povsod narašča.
Potenčne funkcije s sodim pozitivnim eksponentom:

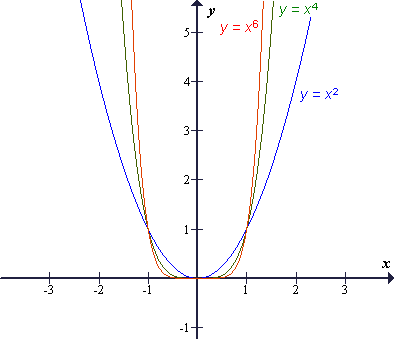
Vsaka funkcija iz te skupine ima naslednje lastnosti:
- D_f = ,
- Z_f = [0, ),
- je soda,
- ima minimum v točki T(0, 0),
- pada na intervalu (−, 0],
- narašča na intervalu [0, ).
Potenčne funkcije z lihim negativnim eksponentom:



Vsaka funkcija iz te skupine ima naslednje lastnosti:
- D_f =  \ {0},
- Z_f =  \ {0},
- je liha,
- ima pol pri x = 0,
- ima navpično asimptoto x = 0,
- ima vodoravno asimptoto y = 0,
- pada na intervalu (−, 0) in na intervalu (0, ).
Potenčne funkcije s sodim negativnim eksponentom:

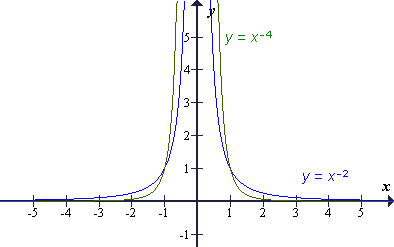
Vsaka funkcija iz te skupine ima naslednje lastnosti:
- D_f = \ {0},
- Z_f = (0, ),
- je vedno pozitivna,
- je soda,
- ima pol pri x = 0,
- ima navpično asimptoto x = 0,
- ima vodoravno asimptoto y = 0,
- narašča na intervalu (−, 0),
- pada na intervalu (0, ).

(Za podrobnejšo razlago lastnosti glej poglavji Funkcije in Lastnosti funkcij.)