Korenska funkcija

Funkcijo n-ti koren (za n ∈

, n > 1) definiramo kot inverz potenčne funkcije f (x) = xⁿ:
n-ti koren iz a je tisto število x, za katero velja, da je xⁿ = a, torej:

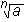= x ⇔ xⁿ = a

Pri tem moramo ločiti dva primera:

Če je n liho število, je potenčna funkcija f (x) = xⁿ bijektivna funkcija f : → , zato inverzna funkcija res obstaja. To pomeni, da za vsak a ∈ obstaja točno eno realno število x, ki ustreza enačbi xⁿ = a.

Če je n liho število, lahko torej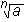 izračunamo za poljuben a ∈ .
Če je n sodo število, pa potenčna funkcija f (x) = xⁿ ni bijektivna funkcija f : → .
Inverzno funkcijo lahko dobimo samo, če se omejimo na nenegativna števila. Vidimo namreč, da je enačba xⁿ = a rešljiva samo, če je a nenegativno realno število. Če je a pozitiven, ima enačba celo dve realni rešitvi, ki se razlikujeta samo za predznak. Po dogovoru za rezultat n-tega korena izberemo nenegativno rešitev te enačbe.

Če je n sodo število, lahko torej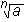 izračunamo samo za nenegativen a ∈ in tudi rezultat je nenegativno število.

Grafi korenskih funkcij

Korenska funkcija je vsaka funkcija, ki jo lahko zapišemo z enačbo oblike f (x) =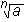 n-ti koren

(kjer je n ∈

, n > 1).
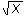Opomba: Za n = 2 korenski eksponent tudi izpuščamo (f (x) = kvadratni koren

).

Kot smo že zapisali, ločimo dve vrsti korenskih funkcij:

Korenske funkcije z lihim korenskim eksponentom:

Vsaka funkcija iz te skupine ima naslednje lastnosti:
- D_f = ,
- Z_f = ,
- narašča povsod,
- v okolici koordinatnega izhodišča je graf funkcije navpičen.
Korenske funkcije s sodim korenskim eksponentom:

Vsaka funkcija iz te skupine ima naslednje lastnosti:
- D_f = [0, ),
- Z_f = [0, ),
- narašča povsod, kjer je definirana,
- v okolici koordinatnega izhodišča je graf funkcije navpičen.

(Za podrobnejšo razlago lastnosti glej poglavji Funkcije in Lastnosti funkcij.)

Potence z necelimi eksponenti

Potence z racionalnimi eksponenti definiramo z naslednjima praviloma: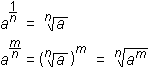

Pri korenskih funkcijah ponavadi privzameno, da je korenski eksponent n naravno število večje od 1, po zgoraj zapisanih pravilih pa lahko definiramo tudi korenske funkcije z drugimi eksponenti.

V praksi lahko korenske funkcije vedno preoblikujemo v potence z necelimi eksponenti, zato tudi ne izpeljujemo posebnih pravil za računanje s koreni. Pravila za računanje s potencami, ki smo jih zapisali pri potenčni funkciji, namreč veljajo tudi za potence z necelimi eksponenti.