Kvadratna funkcija

Kvadratna funkcija je funkcija, ki jo lahko zapišemo z enačbo oblike f (x) = ax² + bx + c, kjer so koeficienti a, b in c poljubna realna števila in je vodilni koeficient a različen od 0.
Enačbo oblike f (x) = ax² + bx + c imenujemo splošna oblika enačbe kvadratne funkcije.

Vsako kvadratno funkcijo lahko zapišemo tudi v temenski obliki: f (x) = a(x − p)² + q.
Števili p in q, ki nastopata v tej obliki, sta koordinati temena kvadratne funkcije. Teme je točka T(p, q), v kateri kvadratna funkcija doseže ekstremno vrednost. Temensko obliko lahko dobimo iz splošne po metodi dopolnjevanja do popolnega kvadrata, lahko pa p in q izračunamo naslednjih formulah:
Teme

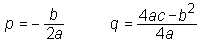
Kvadratno funkcijo lahko zapišemo tudi v ničelni obliki: f (x) = a(x − x₁)(x − x₂).
Števili x₁ in x₂ sta ničli kvadratne funkcije. V splošnem sta to kompleksni števili. Ničelno obliko lahko dobimo iz splošne z razcepom, lahko pa x₁ in x₂ izračunamo po naslednji formuli:
Ničli

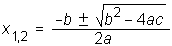
Število, ki v zgornji formuli nastopa pod korenom, imenujemo diskriminanta kvadratne funkcije: D = b² − 4ac. Diskriminanta nam pove, koliko realnih ničel ima kvadratna funkcija:

Če je D > 0, sta obe ničli kvadratne funkcije realni (x₁, x₂ ∈ ).
Če je D = 0, sta števili x₁ in x₂ enaki - kvadratna funkcija ima samo eno realno ničlo (x₁ = x₂ ∈ ).
Če je D < 0, sta obe ničli kvadratne funkcije nerealni (x₁, x₂ ) - graf funkcije ne seka abscisne osi (v realnem koordinatnem sistemu.)

Za ničli kvadratne funkcije f (x) = ax² + bx + c veljata Viètovi formuli:

Viètova formula za vsoto ničel: x₁ + x₂ = −
Viètova formula za produkt ničel: x₁ ∙ x₂ =

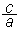
Graf kvadratne funkcije

Graf kvadratne funkcije lahko narišemo postopoma:

najprej narišemo graf y = x²,
potem ta graf raztegnemo z raztegom v smeri osi y za faktor a
nato ga še premaknemo s premikom za vektor (p, q)

Zgled:
Funkcijo f (x) = 2x² − 12x + 16 najprej preoblikujemo v temensko obliko:
f (x) = 2(x − 3)² − 2 in potem narišemo:

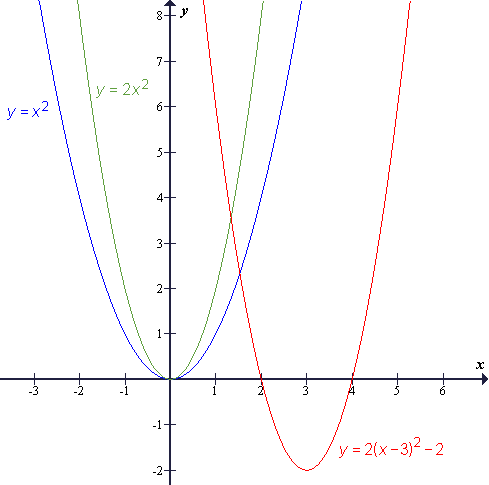
Iz zgornjega postopka vidimo, da vodilni koeficient a odloča o tem, kako je obrnjena kvadratna funkcija:
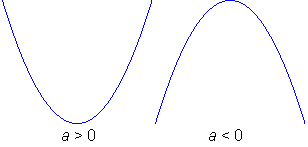
Pomen a

Pri risanju grafa kvadratne funkcije si lahko pomagamo tudi s koeficientom c, ki pomeni presečišče grafa z ordinatno osjo (f (0) = c) in z ničlama x₁ in x₂.

Zgled:
Dana je funkcija f (x) = x² − 2x − 3.
Iz te oblike razberemo odsek na navpični osi: f (0) = −3.
Z dopolnjevanjem do popolnega kvadrata enačbo funkcije preoblikujemo v temensko obliko:
  f (x) = x² − 2x − 3
  f (x) =(x² − 2x + 1) − 1 − 3
  f (x) = (x − 1)² − 4
Iz te oblike razberemo teme: T(1, −4).
Potem enačbo funkcije f še razcepimo, da dobimo ničelno obliko:
  f (x) = x² − 2x − 3
  f (x) =(x + 1)(x − 3)
Iz te oblike razberemo ničli: x₁ = −1, x₂ = 3 in narišemo graf:
   Kvadratna funkcija

Kvadratna enačba

Kvadratna enačba je vsaka enačba, ki jo lahko zapišemo v obliki ax² + bx + c = 0, kjer so koeficienti a, b in c poljubna realna števila in je vodilni koeficient a različen od 0.

Postopek iskanja rešitev kvadratne enačbe je enak postopku iskanja ničel kvadratne funkcije. Torej lahko kvadratno enačbo rešimo z razcepom, ali pa rešitvi x₁ in x₂ izračunamo po že omenjeni formuli:
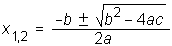
Rešitvi kvadratne enačbe

V obsegu kompleksnih števil je kvadratna enačba vedno rešljiva.

Diskriminanta kvadratne enačbe (D = b² − 4ac) nam pove, kako je z rešljivostjo v množici realnih števil:

Če je D > 0, ima kvadratna enačba dve realni rešitvi (x₁, x₂ ∈ ).
Če je D = 0, ima kvadratna enačba samo eno realno rešitev (x₁ = x₂ ∈ ).
Če je D < 0, kvadratna enačba v realnem ni rešljiva (x₁, x₂ ).

Kvadratna neenačba

Kvadratna neenačba je vsaka neenačba, ki jo lahko zapišemo v obliki ax² + bx + c > 0, kjer so koeficienti a, b in c poljubna realna števila in je vodilni koeficient a različen od 0.
Namesto znaka > lahko nastopa tudi katerikoli od ostalih znakov neenakosti: <, ≤ ali ≥.

Kvadratno neenačbo najlažje rešimo s pomočo grafa ustrezne kvadratne funkcije.