Kazalo poglavij

Polinomi

Krivulje drugega reda

Abecedno kazalo

Racionalne funkcije

Racionalna funkcija je vsaka funkcija, ki jo lahko zapišemo z enačbo oblike: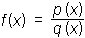
     (kjer je p poljuben polinom, q pa poljuben neničelni polinom).

Oba polinoma lahko tudi razcepimo (po Gaußovem izreku) in tako dobimo razcepljeno obliko racionalne funkcije:
  

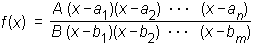
V nadaljevanju bomo izhajali iz predpostavke, da je racionalna funkcija okrajšana, tj. da v razcepljeni obliki ne nastopa isti faktor v števcu in imenovalcu. (Števec in imenovalec bi lahko vsebovala skupni faktor, a v tem primeru bi racionalno funkcijo lahko okrajšali.)

Ničle polinoma v števcu so ničle racionalne funkcije. Ničle polinoma v imenovalcu pa so poli racionalne funkcije. Racionalna funkcija je definirana povsod razen v polih.

Graf racionalne funkcije

Racionalna funkcija je zvezna povsod, kjer je definirana. To pomeni, da se graf racionalne funkcije pretrga samo v polih.
Pri risanju grafa racionalne funkcije upoštevamo naslednja pravila:

• Graf racionalne funkcije, ko gre x proti ±:
  (1) Če je stopnja imenovalca večja od stopnje števca, se graf racionalne funkcije (ko se oddaljujemo od izhodišča koordinatnega sistema) približuje abscisni osi. Torej ima vodoravno asimptoto y = 0.
  
  (2) V splošnem pa števec racionalne funkcije delimo z imenovalcem. Pri tem dobimo polinoma količnik in ostanek. Dobljeni količnik imenujemo asimptotski polinom. Grafu tega polinoma se graf racionalne funkcije približuje, ko se oddaljujemo od izhodišča koordinatnega sistema. Pogosto je asimptotski polinom prve ali ničte stopnje in ima za graf premico. V tem primeru to premico imenujemo glavna asimptota racionalne funkcije.
  Graf racionalne funkcije včasih tudi seka asimptoto (oz. asimptotski polinom) - presečišča so v točkah, kjer je ostanek pri deljenju števca z imenovalcem enak 0.
  
  
• Graf racionalne funkcije v okolici ničle k-te stopnje narišemo enako kot graf polinoma v okolici ničle k-te stopnje.
  
  
• Graf racionalne funkcije v okolici pola k-te stopnje je podoben kot graf potenčne funkcije y = x ^−k (z ustreznim raztegom in premikom).
  To pomeni, da se graf v okolici pola vedno približuje navpični asimptoti, glede predznaka funkcije pa ločimo dve vrsti polov:
  (1) V polih lihe stopnje se predznak funkcije spremeni.
    
  
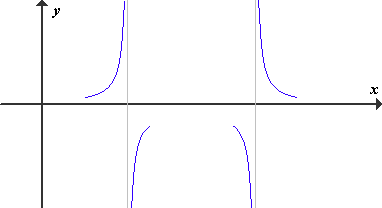
  (2) V polih sode stopnje se predznak funkcije ohrani.
    
  
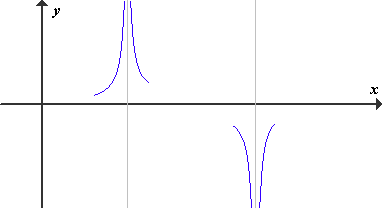
  Torej ugotovimo: Predznak racionalne funkcije se spremeni samo v polih in ničlah lihe stopnje.
  
  

Zgled:
Racionalna funkcij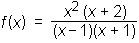a:   ima:

ničli: 0 (II.) in −2
pola: 1 in −1
glavno asimptoto: y = x + 2
graf jo seka pri: x = −2
odsek na ordinatni osi: f(0) = 0

  

Kazalo poglavij

Polinomi

Krivulje drugega reda

Abecedno kazalo