| Kazalo poglavij | Racionalne funkcija | Eksponentna funkcija | Abecedno kazalo |
Krivulje II. reda
Krivulja drugega reda je vsaka množica ravninskih točk, ki ustrezajo enačbi drugega reda:Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
Glavne krivulje drugega reda so krožnica, elipsa, hiperbola in parabola.
Krožnica
Krožnica je množica ravninskih točk, ki so enako oddaljene od danega središča (S). Oddaljenost poljubne točke od središča imenujemo polmer ali radij krožnice (r).Enačba krožnice
Krožnica s središčem S(0, 0) in polmerom r ima enačbo:x2 + y2 = r 2 (enačba krožnice v sredični legi)
Krožnica s središčem S(p, q) in polmerom r ima enačbo:
(x − p)2 + (y − q)2 = r 2 (enačba krožnice v premaknjeni legi)

Glej tudi: Krog in krožnica (geometrijske lastnosti).
Elipsa
Elipsa je množica ravninskih točk, za katere je vsota razdalj do dveh danih točk konstantna. Ti dve točki imenujemo gorišči elipse (G1 in G2).Torej: r1 + r2 = konst.

Elipsa ima dve simetrijski osi (simetrali). Njuno presečišče je središče elipse (S). Točke, kjer simetrali sekata elipso, so temena elipse (T1, T2, T3, T4).
Razdalja od središča do bolj oddaljenega temena se imenuje velika polos elipse (ponavadi jo označimo a), razdalja od središča do manj oddaljenega temena pa se imenuje mala polos elipse (ponavadi jo označimo b).
Gorišči elipse ležita vedno na veliki osi. Razdalja od središča do gorišča se imenuje linearna ekscentričnost elipse (e).
Razmerje med linearnano ekscentričnostjo in veliko polosjo imenujemo numerična ekscentričnost elipse (ε). Numerična ekscentričnost leži vedno na intervalu (0, 1) in nam pove, kakšne oblike je elipsa. Če je ε blizu 0, je elipsa po obliki podobna krogu; če je ε blizu 1, pa je elipsa zelo razpotegnjena (podolgovata).

Enačba elipse
Elipsa v središčni legi ima središče v točki S(0, 0), osi elipse pa ležita na koordinatnih oseh.Taka elipsa ima enačbo:
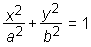
Ponavadi je velika polos a vodoravna, mala polos b pa navpična in veljajo zveze:
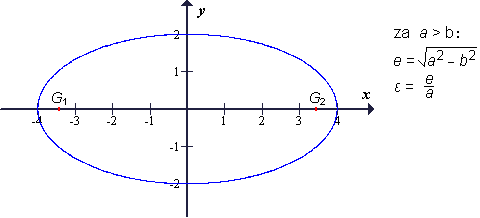
Včasih pa je a < b. To pomeni, da je velika polos navpična (b), mala polos pa vodoravna (a):

Če elipso vzporedno premaknemo tako, da pride središče v točko S(p, q), ima premaknjena elipsa enačbo:
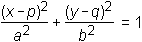
Hiperbola
Hiperbola je množica ravninskih točk, za katere je absolutna vrednost razlike razdalj do dveh danih točk konstantna. Ti dve točki imenujemo gorišči hiperbole (G1 in G2).Torej: |r1 − r2| = konst.

Hiperbola ima dve simetrijski osi (simetrali). Njuno presečišče je središče hiperbole (S). Točki, kjer ena od simetral seka hiperbolo, sta temeni hiperbole (T1 in T2). Druga simetrala ne seka hiperbole.
Razdalja od središča do temena se imenuje polos (tudi realna polos) hiperbole - ponavadi jo označimo a.
Gorišči hiperbole ležita vedno na isti osi kot temeni. Razdalja od središča do gorišča se imenuje linearna ekscentričnost hiperbole (e).
Razmerje med linearnano ekscentričnostjo in realno polosjo imenujemo numerična ekscentričnost hiperbole (ε). Numerična ekscentričnost je vedno večja od 1 in nam pove, kakšne oblike je hiperbola.
Hiperbola ima dve asimptoti: ko se oddaljujemo od izhodišča koordinatnega sistema, se hiperbola približuje tema dvema premicama. Pri risanju asimptot si pomagamo s pravokotnim okvirjem, ki ga določata realna polos a in število b, ki ga imenujemo imaginarna polos in je določeno z enačbo:
a2 + b2 = e2

Enačba hiperbole
Hiperbola v središčni legi ima središče v točki S(0, 0), osi hiperbole pa ležita na koordinatnih oseh.Ločimo dva tipa hiperbol:
Prvi tip: gorišči ležita na abscisni osi, prav tako tudi obe temeni. Hiperbola prvega tipa ima enačbo:

Drugi tip: gorišči ležita na ordinatni osi, prav tako tudi obe temeni. Hiperbola drugega tipa ima enačbo:

Če hiperbolo vzporedno premaknemo tako, da pride središče v točko S(p, q), ima premaknjena hiperbola enačbo:
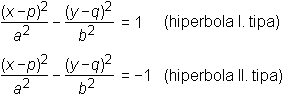
Parabola
Parabola je množica ravninskih točk, ki so enako oddaljene od dane premice vodnice (v) in od dane točke, ki jo imenujemo gorišče (G).Velja torej: r1 = r2

Parabola ima eno simetrijsko os (simetralo). Točko, kjer os seka parabolo, imenujemo teme parabole (T).
Razdaljo med goriščem in vodnico imenujemo parameter parabole (p).
Enačba parabole
Parabola v središčni legi ima teme v točki T(0, 0), os parabole pa leži na eni od koordinatnih osi.Ločimo štiri možnosti:
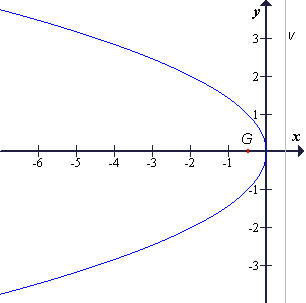
Parabola prvega tipa ima enačbo: y2 = 2px

Parabola drugega tipa ima enačbo: y2 = −2px
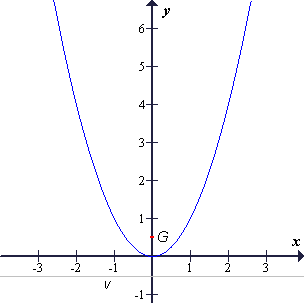
Parabola tretjega tipa ima enačbo: x2 = 2py
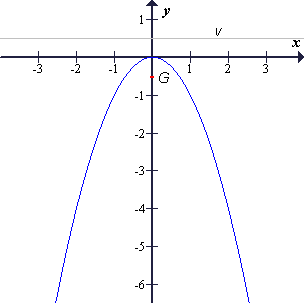
Parabola četrtega tipa ima enačbo: x2 = −2py
Če parabolo vzporedno premaknemo tako, da pride teme v točko T(x0, y0), ima premaknjena parabola enačbo:
(y − y0)2 = 2p(x − x0) (parabola I. tipa)
(y − y0)2 = −2p(x − x0) (parabola II. tipa)
(x − x0)2 = 2p(y − y0) (parabola III. tipa)
(x − x0)2 = −2p(y − y0) (parabola IV. tipa)
Graf kvadratne funkcije f (x) = ax2 + bx + c je vedno parabola III. ali IV. tipa. Parameter te parabole je enak
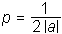
| Kazalo poglavij | Racionalne funkcija | Eksponentna funkcija | Abecedno kazalo |