Kazalo poglavij

Koti

Simetrija - simetrale

Abecedno kazalo

Krog in krožnica

Krožnica je množica ravninskih točk, ki so enako oddaljene od dane točke S. Točko S imenujemo središče krožnice, razdalja med središčem in poljubno točko na krožnici pa je polmer ali radij krožnice.

Krožnici sta skladni, če in samo če imata enako dolga polmera.

Tetiva je daljica, ki povezuje dve točki krožnice.
Premer ali diameter je najdaljša tetiva. Premer poteka skozi središče in je dvakrat daljši od polmera: d = 2r.
Točki, ki sta krajišči enega od premerov, sta diametralni točki krožnice.

Zgled:
  
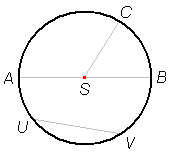
AB = premer (točki A in B sta diametralni)
SC = polmer
UV = tetiva

Del krožnice omejen z dvema točkama imenujemo krožni lok.
Krožna loka, ki imata isti krajišči in skupaj sestavljata celotno krožnico, imenujemo dopolnilna loka.

Krog s središčem S in polmerom r je množica ravninskih točk, katerih oddaljenost od središča je manjša ali enaka r.
To pomeni, da je krog del ravnine omejen s krožnico.

Glej tudi:
Krožnica kot krivulja drugega reda
Obseg in ploščina

Medsebojna lega krožnice in premice

Krožnica in premica, ki ležita v isti ravnini, imata lahko tri različne medsebojne lege:

• Če nimata nobene skupne točke, pravimo, da je premica mimobežnica.
  
  
• Če imata eno skupno točko, pravimo, da je premica tangenta (dotikalnica) krožnice.
  
  
• Če imata dve skupni točki, pravimo, da je premica sekanta krožnice.
  
  

Talesov izrek o kotu v polkrogu

Za kot v polkrogu velja Talesov izrek:
Če vrh kota φ leži na polkrožnici, kraka pa potekata skozi krajišči premera, potem je φ pravi kot.

  
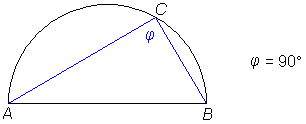
Uporabljamo tudi drugačen način izražanja:
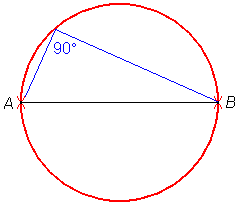
Iz katerekoli točke na polkrožnici (razen iz A in B) vidimo premer AB pod zornim kotom 90°.

Množica vseh ravninskih točk, iz katerih se vidi daljico AB pod zornim kotom 90°, je krožnica s premerom AB (brez krajišč premera).

  

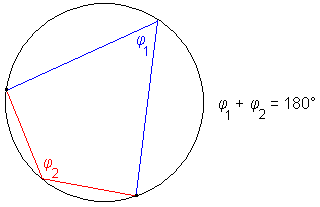
Izrek o središčnem in obodnem kotu

Dana je krožnica in na njej krožni lok AB.
Središčni kot nad lokom AB je kot α, ki ima vrh v središču krožnice, njegova kraka potekata skozi krajišči loka, lok AB pa leži v kotu α.
Obodni kot nad lokom AB je kot φ, ki ima vrh na dopolnilnem loku loka AB, njegova kraka potekata skozi krajišči loka, lok AB pa leži v kotu φ.

  
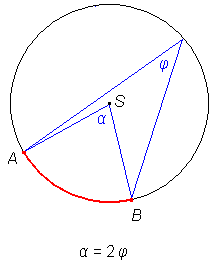
Velja izrek o središčnem in obodnem kotu:
Središčni kot je dvakrat večji od obodnega kota nad istim lokom.
Vsi obodni koti nad istim lokom so med sabo skladni.
Klikni tukaj za gibljivi prikaz.


Obodna kota nad dopolnilnima lokoma sta med sabo suplementarna.

  


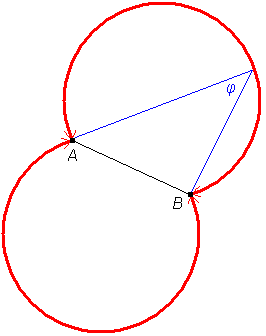
Množica vseh ravninskih točk, iz katerih vidimo daljico AB pod danim zornim kotom φ, je sestavljena iz dveh skladnih krožnih lokov (brez krajišč).

  

Kazalo poglavij

Koti

Simetrija - simetrale

Abecedno kazalo