| Kazalo poglavij | Togi premiki in skladnost | Krog in krožnica | Abecedno kazalo |
Koti
Kot je del ravnine omejen z dvema poltrakoma, ki izhajata iz skupnega izhodišča.Ta dva poltraka imenujemo kraka kota, skupno izhodišče pa imenujemo vrh kota.
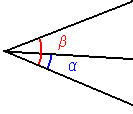
Zgled: dana poltraka omejujeta v ravnini konveksni kot α in konkavni kot β:

Kot vidimo, pripada poljubnemu konkavnemu kotu vedno točno en ustrezni konveksni kot. Zato konkavnih kotov v geometriji ponavadi ne obravnavamo posebej - lastnosti konkavnih kotov so posledice lastnosti ustreznih konveksnih kotov.
Zato bomo v geometriji praviloma privzeli, da beseda »kot« pomeni »konveksni kot«.
Za kot v splošnejšem pomenu besede glej poglavje Trigonometrijske funkcije - razširitev pojma kot.
Kot poseben primer dodamo v množico vseh kotov ničelni kot, ki je pravzaprav samo en poltrak, in polni kot, ki pomeni celotno ravnino.
Kot, ki ima za kraka dopolnilna poltraka, imenujemo iztegnjeni kot. Geometrijsko je enak polravnini.
Primerjanje kotov po velikosti
Če želimo primerjati dva kota po velikosti, preslikamo prvega na drugega s togim premikom, tako da se preslika vrh prvega na vrh drugega in en krak prvega na krak drugega kota. Pri tem se notranjosti kotov lahko delno ali popolnoma prekrijeta. Če se popolnoma prekrijeta sta kota skladna, sicer pa je manjši tisti kot, ki leži znotraj drugega.Zgled: α < β
Posebne lege in vrste kotov
Sovršna kota sta (konveksna) kota, ki imata za krake dopolnilne poltrake.Sosednja kota ali kota v sosednji legi sta kota, ki imata skupen vrh in enega od krakov.
Sokota sta (konveksna) kota, ki imata skupen vrh in enega od krakov, ostala dva kraka pa sta dopolnilna poltraka.

Pravi kot je kot, ki je skladen s svojim sokotom.
Ostri kot je kot, ki je manjši od svojega sokota.
Topi kot je (konveksni) kot, ki je večji od svojega sokota.
Merjenje kotov
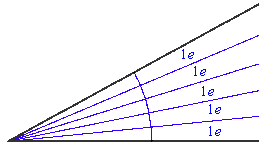
Velikost kota je število, ki pove, koliko enotskih kotov potrebujemo, da dani kot popolnoma pokrijemo. Pri tem enotske kote nanašamo tako, da imata po dva en krak skupen in da imajo vsi vrh v vrhu danega kota. Če se postopek pokrivanja ne izide s celim številom enotskih kotov, nadaljujemo z manjšimi enotami (desetinkami, stotinkami, šestdesetinkami, ipd).Zgled: kot, ki meri 5 enot:
Enote, ki jih v geometriji najpogosteje uporabljamo za merjenje kotov, so stopinje. Ena stopinja je definirana kot stoosemdesetinka iztegenjenega kota oziroma tristošestdesetinka polnega kota.
Ena stopinja se deli na 60 minut, ena minuta se naprej deli na 60 sekund. V novejšem času pogosto uporabljamo tudi izražanje kotov v decimalni obliki, npr.:
12°45' = 12.75°
V matematični analizi uporabljamo poleg stopinj tudi radiane.
Kota α in β sta suplementarna, če velja α + β = 180°.
Kota α in β sta komplementarna, če velja α + β = 90°.
Princip kotov z vzporednimi kraki
(Konveksna) kota, ki imata paroma vzporedne krake, sta skladna ali pa suplementarna.Če sta pri tem oba para krakov usmerjena v isto smer, sta kota skladna.
Če sta pri tem oba para krakov usmerjena v nasprotno smer, sta kota skladna.
Če je en par krakov usmerjen v isto smer, drugi par pa v nasprotno, sta kota suplementarna.

Princip kotov s pravokotnimi kraki
(Konveksna) kota, ki imata paroma pravokotne krake, sta skladna ali pa suplementarna.Če leži vrh enega kota v notranjosti drugega, sta kota suplementarna.
Če leži vrh enega kota zunaj drugega, sta kota skladna.

| Kazalo poglavij | Togi premiki in skladnost | Krog in krožnica | Abecedno kazalo |