Kazalo poglavij

Logaritemska funkcija

Ciklometrične funkcije

Abecedno kazalo

Trigonometrijske funkcije

Razširitev pojma kot

Kot v geometriji definiramo kot del ravnine, omejen z dvema poltrakoma, ki imata skupno izhodišče.
Ta definicija je primerna za kote od 0° do 360°.
Na splošno si kot raje predstavljamo kot zasuk: v koordinatnem sistemu pozitivni del abscisne osi zasukamo okoli koordinatnega izhodišča. Pri taki definiciji kota lahko govorimo tudi o kotih, ki so večji od 360°, pa tudi o kotih, ki so manjši od 0° (zasuk v negativni smeri).



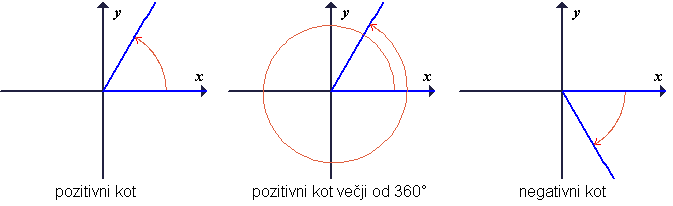
Pozitivni del abscisne osi imenujemo fiksni krak kota, zasukani poltrak pa gibljivi krak kota.

Pri sukanju gibljivega kraka okoli izhodišča koordinatnega sistema potuje točka A(1, 0) po enotski krožnici. Dolžina poti (d), ki jo ta točka opravi pri določenem kotu oziroma zasuku, se imenuje velikost kota v radianih.



Ker je obseg enotske krožnice enak 2π, vidimo, da je 360° = 2π radianov.
Pri radianih po dogovoru izpuščamo oznako enote, torej pišemo kar
  360° = 2π          180° = π      itd.

Definicije trigonometrijskih (kotnih) funkcij

Sinus kota je ordinata točke T, v kateri gibljivi krak kota seka enotsko krožnico.
Kosinus kota je abscisa točke T, v kateri gibljivi krak kota seka enotsko krožnico.
Tangens kota je ordinata točke U, v kateri nosilka gibljivega kraka kota seka navpično premico x = 1.
Kotangens kota je abscisa točke V, v kateri nosilka gibljivega kraka kota seka vodoravno premico y = 1.



Oznake:
sinus kota x označujemo z oznako sin x,
kosinus kota x označujemo z oznako cos x,
tangens kota x označujemo z oznako tg x   (ali tudi tan x),
kotangens kota x označujemo z oznako ctg x   (ali tudi cot x, cotan x, ctan x ali ctn x).

(Glej tudi: Definicije kotnih funkcij v pravokotnem trikotniku.)

Osnovne zveze med kotnimi funkcijami

Med kotnimi funkcijami istega kota x veljajo zveze:

  

Opomba: Potence kotnih funkcij po dogovoru označujemo (v Evropi) na krajši način: (sin x)ⁿ = sinⁿ x. Tak način označevanja smo uporabili tudi v zgornjih zvezah.
Po tem dogovoru pomeni tudi zapis sin⁻¹ x = (sin x)⁻¹   (in ne arkus sinus x, kar ta oznaka pomeni v nekaterih drugih koncih sveta).

Grafi in lastnosti trigonometrijskih funkcij

Opomba: Pri risanju grafov kotnih funkcij vedno privzamemo, da je argument x kot v radianih.

• Funkcija f (x) = sin x
    
  D_f = 
  Z_f = [−1, 1]
  Ničle: x = kπ ;   k ∈ 
  Maksimumi: M( + 2kπ, 1) ;   k ∈ 
  Minimumi: m(− + 2kπ, −1) ;   k ∈ 
  
  
  
• Funkcija f (x) = cos x
    
  D_f = 
  Z_f = [−1, 1]
  Ničle: x =  + kπ ;   k ∈ 
  Maksimumi: M(2kπ, 1) ;   k ∈ 
  Minimumi: m(π + 2kπ, −1) ;   k ∈ 
  
  
  
• Funkcija f (x) = tg x
  
    
  
  D_f =  \ { + kπ ;  k ∈ }
  Z_f = 
  Ničle: x = kπ ;   k ∈ 
  Poli: x =  + kπ ;   k ∈ 
  
  
  
• Funkcija f (x) = ctg x
  
    
  
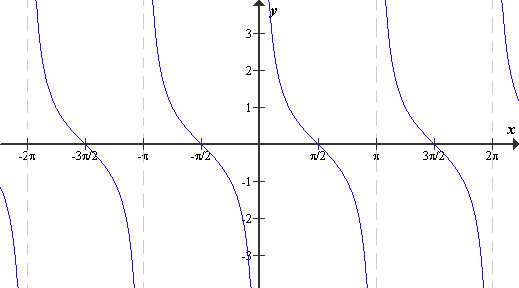
  D_f =  \ {kπ ;  k ∈ }
  Z_f = 
  Ničle: x =  + kπ ;   k ∈ 
  Poli: x = kπ ;   k ∈ 
  

Pomembnejše formule

Adicijski izreki

   sin(x + y) = sin x cos y + cos x sin y
   sin(x − y) = sin x cos y − cos x sin y
   cos(x + y) = cos x cos y − sin x sin y
   cos(x − y) = cos x cos y + sin x sin y
   

Funkcije dvojnih kotov

   sin 2x = 2 sin x cos x
   cos 2x = cos² x − sin² x
   

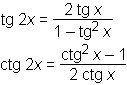
Faktorizacija kotnih funkcij

   sin x + sin y = 2 sin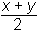 cos
   sin x − sin y = 2 sin cos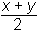
   cos x + cos y = 2 cos 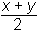cos
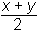   cos x − cos y = −2 sin sin

Razčlenjevanje kotnih funkcij

   sin x sin y = −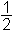  (cos(x + y) − cos(x − y))
   cos x cos y = 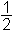 (cos(x + y) + cos(x − y))
   sin x cos y = 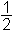 (sin(x + y) + sin(x − y))

Kazalo poglavij

Logaritemska funkcija

Ciklometrične funkcije

Abecedno kazalo