Ciklometrične funkcije

Ciklometrične funkcije so inverzi trigonometrijskih funkcij. Imenujemo jih tudi krožne funkcije ali arkus funkcije. Ker nobena od trigonometrijskih funkcij ni bijektivna, so ciklometrične funkcije samo njihovi delni inverzi.

Poznamo torej štiri ciklometrične funkcije:
arkus sinus, ki ga označimo arc sin (ali tudi arcsin, asin, ...),
arkus kosinus, ki ga označimo arc cos (ali tudi arccos, acos, ...),
arkus tangens, ki ga označimo arc tg (ali tudi arctan, atan, ...),
arkus kotangens, ki ga označimo arc ctg (ali tudi arccot, actn, ...).

Rezultati ciklometričnih funkcij so koti, ki jih praviloma navajamo v radianih.

Arkus sinus

Arkus sinus števila a je število x, za katero velja sin x = a, torej:
arc sin a = x ⇔ sin x = a

Če je a ∈ [−1, 1], potem ima enačba sin x = a neskončno mnogo realnih rešitev. Po dogovoru je rezultat funkcije arkus sinus po absolutni vrednosti najmanjša rešitev enačbe sin x = a.
Če je a ni element

[−1, 1], potem enačba sin x = a sploh nima realnih rešitev.
To pomeni, da je funkcija arkus sinus definirana samo za a ∈ [−1, 1] .

Graf funkcije arkus sinus dobimo tako, da graf funkcije sinus prezrcalimo čez simetralo lihih kvadrantov. Dobljena množica točk pa ni graf funkcije, pač pa množica vseh rešitev enačbe sin y = x. Graf funkcije arkus sinus je samo del te množice - na sliki označen z rdečo barvo.

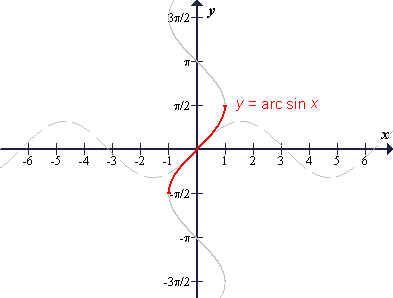
Arkus kosinus

Arkus kosinus števila a je število x, za katero velja cos x = a, torej:
arc cos a = x ⇔ cos x = a

Če je a ∈ [−1, 1], potem ima enačba cos x = a neskončno mnogo realnih rešitev. Po dogovoru je rezultat funkcije arkus kosinus najmanjša nenegativna rešitev enačbe cos x = a.
Če je a ni element

[−1, 1], potem enačba cos x = a sploh nima realnih rešitev.
To pomeni, da je funkcija arkus kosinus definirana samo za a ∈ [−1, 1] .

Graf funkcije arkus kosinus dobimo tako, da graf funkcije kosinus prezrcalimo čez simetralo lihih kvadrantov. Dobljena množica točk pa ni graf funkcije, pač pa množica vseh rešitev enačbe cos y = x. Graf funkcije arkus kosinus je samo del te množice - na sliki označen z rdečo barvo.

Arkus tangens

Arkus tangens števila a je število x, za katero velja tg x = a, torej:
arc tg a = x ⇔ tg x = a

Enačba tg x = a ima vedno neskončno mnogo realnih rešitev. Po dogovoru je rezultat funkcije arkus tangens po absolutni vrednosti najmanjša rešitev enačbe tg x = a.

Graf funkcije arkus tangens dobimo tako, da graf funkcije tangens prezrcalimo čez simetralo lihih kvadrantov. Dobljena množica točk pa ni graf funkcije, pač pa množica vseh rešitev enačbe tg y = x. Graf funkcije arkus tangens je samo del te množice - na sliki označen z rdečo barvo.

Arkus kotangens

Arkus kotangens števila a je število x, za katero velja ctg x = a, torej:
arc ctg a = x ⇔ ctg x = a

Enačba ctg x = a ima vedno neskončno mnogo realnih rešitev. Po dogovoru je rezultat funkcije arkus kotangens najmanjša nenegativna rešitev enačbe ctg x = a.

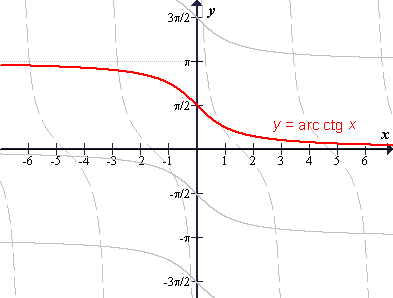
Graf funkcije arkus kotangens dobimo tako, da graf funkcije kotangens prezrcalimo čez simetralo lihih kvadrantov. Dobljena množica točk pa ni graf funkcije, pač pa množica vseh rešitev enačbe ctg y = x. Graf funkcije arkus kotangens je samo del te množice - na sliki označen z rdečo barvo.

Kazalo poglavij

Trigonometrijske funkcije

Geometrija

Abecedno kazalo