Osnove geometrije

Osnovni pojmi geometrije so točka, premica, ravnina in prostor. Povezujejo jih naslednje najpomembnejše lastnosti (aksiomi):

Skozi poljubni dve točki poteka točno ena premica.

Definicija: Točke, ki ležijo na isti premici, imenujemo kolinearne točke.
Skozi poljubne tri nekolinearne točke poteka točno ena ravnina.

Definicija: Točke, ki ležijo na isti ravnini, imenujemo komplanarne (koplanarne) točke.
Če imata premica in ravnina več kot eno skupno točko, potem leži celotna premica v tej ravnini.
Če se dve ravnini sekata, potem je njun presek premica.

Definicija: Premici sta vzporedni, če ležita v isti ravnini in nimata nobene skupne točke (se ne sekata). Poleg tega pravimo, da je vsaka premica vzporedna sama sebi.
Evklidov aksiom o vzporednici: Skozi poljubno točko poteka točno ena vzporednica k dani premici.

Razdalja

Razdaljo med točkama A in B označimo z oznako |AB| oziroma AB.
Razdalja podaja osnovni odnos med dvema točkama.

Lastnosti razdalje
Za poljubne točke A, B in C velja:

|AB| ≥ 0 (razdalja je nenegativno število)
|AB| = 0 ⇔ A = B (razdalja med A in B je enaka 0, samo če oznaki A in B označujeta isto točko)
|AB| = |BA| (simetričnost)
|AB| ≤ |AC| + |CB| (trikotniška neenakost)

Če v zadnji lastnosti za tri različne točke A, B in C velja enačaj: |AB| = |AC| + |CB|, potem točka C leži na premici, ki poteka skozi A in B, in sicer med točkama A in B.

Deli premice, ravnine in prostora

Daljica AB je množica točk, ki na premici skozi A in B ležijo med točkama A in B. Daljica AB vključuje tudi točki A in B, ki ju imenujemo krajišči daljice.

Točka T, ki leži na premici p, razdeli premico na dva dela. Vsakega od njiju imenujemo poltrak. Točka T je izhodišče obeh poltrakov. Običajno privzamemo, da je izhodišče vključeno v poltrak.
Poltraka, ki imata isto izhodišče in skupaj sestavljata premico, imenujemo dopolnilna poltraka.

Premica p, ki leži v ravnini, deli to ravnino na dve polravnini. Polravnina lahko robno premico p vključuje (zaprta polravnina) ali pa tudi ne (odprta polravnina).

Ravnina deli prostor na dva polprostora. Tudi v tem primeru lahko govorimo o zaprtem ali odprtem polprostoru (zaprti vsebuje robno ravnino, odprti pa ne).

Konveksnost

Množica M je konveksna, če lahko poljubni točki A in B iz te množice povežemo z daljico, ki v celoti leži v množici M.
Konveksna množica

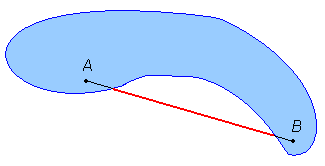
Množica, ki ni konveksna, je konkavna. To pomeni, da obstaja v množici (vsaj en) par točk, ki ju povezuje daljica, ki ne leži v celoti v dani množici.
Konkavna množica

Kazalo poglavij

Ciklometrične funkcije

Togi premiki in skladnost

Abecedno kazalo