TEMELJNI IZREK FILOTAKSE

Izrek ureja celotno geometrijsko povezavo med dvema konceptoma; med vidnim nasprotnim parastihijskim parom (m, n) in divergentnim kotom d. Izrek določa bistvene lastnosti mrež, ki se jih uporablja v večini pojasnjevalnih modelov in pri poizkusih, da bi razumeli filotakso.

PREDSTAVITEV IZREKA

ULOMKI V FILOTAKSI POVEZANI Z FIBONACCIJEVIM KOTOM

OSNOVNA OBLIKA IZREKA FILOTAKSE:
Naj bosta (m, n) parastihijski par, kjer sta m in n praštevili v sistemu z divergentnim kotom d. Naslednji lastnosti sta si ekvivalentni:
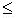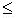1. Obstajata natanko določeni celi števili v in u, 0 v < n , in 0 u < m, tako da je | mv - nu | = 1 in d 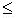1/2. Vrednost divergentnega kota d je znotraj zaprtega intervala [u/m, v/n];
2. Parastihijski par (m, n) je viden in nasproten.

Dokaz tega izreka je osnovan na elegantni posledici vidnih nasprotnih parastihijskih parov. Posledica je, da je par (m, n) viden, če velja |m(nd) - n(md)| = 1, kjer pomeni oznaka (x) številu x najbližje celo število.

Dokaz izreka

POSEBNA OBLIKA IZREKA FILOTAKSE:
Zaporedje normalne filotakse
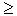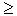Fibonaccijev tip zaporedja J‹1, t, t +1, 2t +1, 3t +2, 5t +3, …›, kjer sta t in J celi števili; t2, J1.
J množi vse člene zaporedja, in je Nt,k = Fk t + Fk - 1 splošni člen:
parastihijski par (JNt,k, JNt,k + 1 ) je viden in nasproten, če je vrednost divergentnega kota d znotraj intervala, katerega krajišči sta Fk / JNt,k in Fk + 1 / JNt,k + 1 .

Iz tega sledi, da je za poljubni celi števili t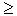2 in J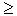1 divergenca znotraj intervala [1/J(t + 1), 1/Jt], če in samo če je parastihijski par J(t, t +1) viden in nasproten.
Divergenca je znotraj intervala [1/J(t + 1), 2/J(2t + 1)], če in samo če je J(2t + 1, t + 1) vidni nasprotni parastihijski par. Če nadaljujemo z dodajanjem števcev in imenovalcev v zadnji interval vidimo, da je divergenca znotraj intervala [3/J(3t + 2), 2/J(2t + 1)], če in samo če je J(2t + 1, 3t +2) vidni nasprotni parastihijski par in tako dalje.

Fibonaccijevo zaporedje, za t = 2 in J = 1, nam da naslednji izrek, imenovan po Adlerju:
Parastihijski par (Fk, Fk + 1) je viden in nasproten, če in samo če je d enak bodisi Fk-2 /Fk ali Fk-1 /Fk +1 ali pa je med tema dvema vrednostima.

Od prej vemo, da se kvocienta v Adlerjevem izreku približujeta 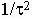, ko k narašča. Slednje število je v intervalu definiramo s kvocienti. Poglejmo si Adlerjev izrek na primeru:
(3, 5) je vidni nasprotni par, če je d znotraj intervala [2/5, 1/3],
(8, 5) je vidni nasprotni par, če je d znotraj intervala [3/8, 2/5],
(13, 8) je vidni nasprotni par, če je d znotraj intervala [3/8, 5/13].
Drug primer si poglejmo na cvetu sončnice: Če je opazen parastihijski par [21, 34] na sončnici oblikovan iz listkov ali semen, potem vemo, da je divergentni kot za ta cvet blizu (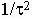)360°, to je znotraj intervala [8/21, 13/34], se pravi [137.14°, 137.65°]. Obrat tega je, če se merjene vrednosti divergentnega kota kopičijo okoli 137.5°; potem je vidni nasprotni par sistema sestavljen iz zaporednih Fibonaccijevih števil.

Podobno kot v Adlerjevem izreku dobimo rezultat še za Lucasovo zaporedje, določimo vrednosti za Lucasovo zaporedje v zaporedju normalne filotakse: t = 3 in J = 1. primer

Opazimo lahko, da za vrednosti t = 1 in J = 1, dobimo kot 222.5°, ki je komplementaren Fibonaccijevem kotu. primer

Botanični pomen za J > 1 je v obstoju mnogopernatosti in večstebelnosti.

Zaporedje posebne filotakse
Fibonaccijev tip zaporedja ‹2, 2t +1, 2t +3, 4t +4, 6t +7, 10t +11,›, kjer je t celo število,t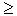 2.
Parastihijski par (2t + 1, 2t +3) je viden in nasproten, če je vrednost divergentnega kota d znotraj intervala, katerega krajišči sta t / (2t+1) in (t +1) / (2t+3).


par (4t +4, 2t +3) je viden in nasproten, če in samo če je d znotraj intervala [(2t+1)/(4t +4), (t +1)/(2t +3)] in tako dalje.

Primer za t=2

Splošni obliki končnih točk intervala za normalno ter za posebno obliko filotakse sta Fk / JNt,k ter Nt,k / (2Fkt + Fk+1 + Fk-1). Limitna divergentna kota, ko gre k proti neskončnosti, pri normalni in posebni filotaksi sta 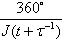ter .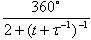


/\ /\ /\ /\
|| || || ||