Za bolj nazorni prikaz narišemo spiralo z majhnim nagibom,
kot na sliki spodaj. Postavimo točke na njo, točke so za 137.5° oddaljene ena
od druge. Točke zaporedno označimo. Te točke lahko predstavljajo mesta na valjastem
steblu, kjer rastejo listi, preoblikovano v stožec, gledan od zgoraj, to pa
je projicirano na ravnino. Alternativno, lahko predstavljajo cvet v spiralni
mreži tako kot na primer notranjost cveta pri marjetici.
Sedaj zbrišemo spiralo in naredimo več kopij množic točk.
Na vsako kopijo narišemo družino x-spiral,
ki imajo isto os in potekajo skozi točke tako, da se razdelijo na posamezne
množice točk. To lahko naredimo z povezovanjem točk tako, da se številke na
njih razlikujejo za 2, 3, … .
Spodnje slika kažejo primere za x = 2, x = 3, x
= 5 in x = 8, kjer se točke na poljubni spirali razlikujejo za
2, 3, 5 in 8 in nam dajo 2- parastihije, 3-parastihije, 5 - parastihije in 8
- parastihije. Lahko opazimo, da ima število x lahko le naslednje
vrednosti: 1, 2, 3, 5, 7, 8, 11, 12, 13, 14, 17, … . Števila ni v tej urejeni
vrsti števil, če je večkratnik števila x in če določa že eno izmed
x-parastihij (npr. za x=4 je že določena z 2 - paristihijmi,
zato 4 ni med vrednostmi x).
x=2
x=3
x=5
x=8
Sedaj položimo dve kopiji točk, katerih družine spiral zavijajo v nasprotnih si smereh ena vrh druge in pogledamo take parastihijske pare, pri katerih se v presečišču poljubnih dveh spiral nahaja točka iz množice. To nam da vidne nasprotne parastihijske pare. Pokaže se, da so edini možni vidni nasprotni parastihijski pari (2, 1), (2, 3), (5, 3), (5, 8), … , vsi pa so sestavljeni iz zaporednih Fibonaccijevih števil.
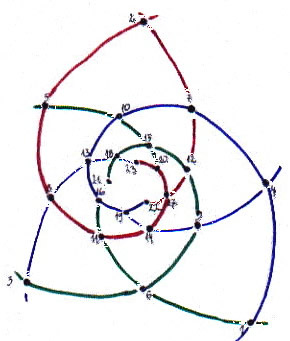 parastihijski
par (3,5)
parastihijski
par (3,5)
ULOMKI V FILOTAKSI POVEZANI Z FIBONACCIJEVIM KOTOM
/\ /\ /\ /\
|| || || ||