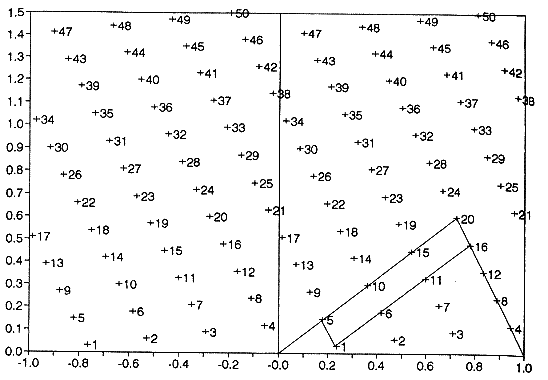
Slika 31: Cilindrična predstavitev mreže točk z divergenco d = 17/72. Koordinate točk n v pasu S so (nd-(nd), nr)
Filotakse in Fareyeve vrste
Vidni parastihijski pari
Filotakse
in Fareyeve vrste
Ogledali si bomo osnovne koncepte filotaks v splošnem okviru, ki so pripeljali
do osnovne oblike temeljnega izreka filotakse. Predstavljena bo teorija, ki
bo zadevala splošni vidik mrež, ki pa v podrobnostih da rezultate iz filotakse.

Slika 31: Cilindrična predstavitev mreže točk z divergenco d =
17/72. Koordinate točk n v pasu S so (nd-(nd), nr)
Slika
31 nam kaže normalno točkovno mrežo. Mreža je zgrajena iz divergentnega
kota d = 85°, ali 85 / 360 = 17 / 72. To je abscisa točke 1, vzeto število
je vedno manjše od 1/2. Koordinate točk n = 1, 2, 3, …, so (nd
- k, nr), kjer je dvig r ordinata točke 1 in k je
poljubno celo število. Osredotočimo se na točke, katerih abscisa je med vključno
- 0.5 in + 0.5, vključno z neskončnim vertikalnim pasom, ki ga označimo z S.
Na tem odseku mreže so (nd - (nd), nr) koordinate točke n,
kjer je (x) najbližje celo števil k x. Če je nd ravno polovica
lihega števila, potem je (nd) lahko [nd] ali [nd] + 1,
kjer je [x] celi del od x. Vrednost nd - (nd) je
sekundarna divergenca točke n. Za poljubno celo število N je urejena
množica ulomkov (kd)/k < 1/2, k = 1, 2, 3, … N, označimo
jo z A. Bližje kot je točka x vertikalni osi, bližja je vrednost
(xd) / x k d. Ulomek je znan kot filotaksin ulomek ali filotaksa,
ki je približek divergence d. Če zvijemo vertikalen pas S v obliko
valja, potem (xd) predstavlja število obratov, od točke 0 do x,
na rodovni spirali okrog valja. Če vzamemo poljubni dve točki x in y
na vsaki strani vertikale, potem je d med (xd) / x in (yd)
/ y.
Družino parastihij določimo tako, da potegnemo daljico med dvema točkama mreže
x in y in nobena točka mreže ne sme ležati med tema dvema točkama.
Družine parastihij m = |x - y| so vzporedne, enako oddaljene
daljice, ki delijo mrežne točke in jih povezujejo od m do n.
Poljubni dve taki družini, ki vsebujeta m in n daljice, imenujemo
vsako posebej parastihijski par (m, n). Če imajo daljice v eni družini
pozitiven nagib, v drugi pa negativen nagib, pravimo, da je par nasproten. Par
(m, n) je viden, če obstaja mrežna točka na vsakem presečišču poljubnih
dveh daljic para.
Na primer na Sliki 31 je par (5, 7) obraten, 7 in 5 se
pojavita vsak na svoji strani vertikalne osi znotraj pasa S, en z absciso
med - 1/2 in 0, drugi z absciso med 0 in 1/2 . Par ni viden, ker gre daljica
skozi točke 7, 14, 21, 28, … in ne seka v mrežni točki daljice, ki poteka skozi
točke 5, 10, 15, 20, … . Par (5, 13) ni obraten in tudi ne viden. Par (5, 14)
ni obraten, je pa viden. Par (17, 4) je viden in obraten.
Fareyevo zaporedje F(N) za N = 1, 2, 3, …, je abstraktna
množica racionalnih števil p/q, med 0 in 1, 0p
q
N
, urejena v naraščajočem zaporedju.
Na primer:
F(1) je zaporedje 0/1, 1/1.
F(2) je zaporedje 0/1, 1/2, 1/1.
F(3) je zaporedje 0/1, 1/3, 1/2, 2/3, 1/1.
F(4) je zaporedje 0/1, 1/4, 1/3, 1/2, 2/3, 3/4, 1/1.
Glavne lastnosti:
(1) Če so p1 / q1, p2
/ q2 in p3 / q3 zaporedni
v F(N) za neki N, potem je | p1q2
- q1p2 | = 1 in p2 / q2
= (p1 + p3)/( q1 + q3);
(2) Če je | p1q2 - q1p2
| = 1 potem sta p1 / q1 in p2
/ q2zaporedna v F(N) za max(q1,
q2) N < q1 + q2
in sta ločena z enim samim elementom (p1 + p2)/(
q1 + q2), imenovanim Fareyeva vsota ulomkov
p1 / q1 in p2 / q2
Prvotna karakterizacija vidnega para (m, n), podana v Izreku 1, vključuje relacijo |m(nd) - n(md)| = 1. O tej relaciji je razpravljalo več botanikov in dobili so podobne zveze kot v teoriji Fareyevih zaporedij. Postalo je jasno, da lahko s temi zaporedji preiskujemo prostorska razmerja med listi poganjkov, ki so predstavljeni z točkovno mrežo.
Vidni
parastihijski pari
Izrek
1.
V normalni mreži z divergenco d je parastihijski par (m, n)
viden, če in samo če sta m in n taki točki, da je |m(nd)
- n(md)| = 1.
V nekaterih primerih imata lahko (nd) ali (md) dve možni vrednosti.
Če za katero od teh vrednosti drži relacija |m(nd) - n(md)|
= 1, potem je par (m, n) viden. V paru (m, n) sta
m in n tuji si števili, to ne pomeni, da je posledično (m,
n) viden, kar smo že videli na primeru (7, 5) na Sliki
31 . Za par (7, 5) obstaja par celih števil u = 3 in v = 2,
tako da je |mv - nu| = 1. Obstaja še en par celih števil (7d)
= 2 in (5d) = 1, za katere se 7(5d) - 5(7d) razlikuje za 1 in
je divergenca med (5d)/5 in (7d)/7, kot je bilo pričakovano. Divergenca
ni med v/n =2/5 in u/m = 3/7.
Izrek 1, temeljni izrek filotakse, nam pokaže, da nam par (m, n), če
je viden in nasproten, prinese isto relacijo za ista cela števila.
Izrek
2.
Parastihijski par (m, n) je viden in nasproten, če in samo če obstajata
taki dve celi števili v in u, tako da je 0 v
< n in 0
u
< m ter | mv - nu | = 1 in tako divergenca d
1/2 leži na ali
med vrednostima u/m in v/n.
V splošnem, če zanemarimo omejitve glede števil v in u, če vzamemo,
da sta m in n tuji si števili in rešitev diofantske enačbe mv
- nu = 1, potem dobimo neskončno mnogo rešitev. Omejitev 0
v < n in 0
u < m nam da vedeti, da obstaja le končno mnogo rešitev. Bolj
natančno u/m in v/n sta zaporedna v F(N) za max(m,
n)
N
< m + n. Divergentni kot d leži med takima dvema zaporednima
ulomkoma, da za u in v obstaja le ena izbira, kot nam pove že
Izrek 2.
Dokaz za Izrek 2 lahko osnujemo na elementarnih lastnostih podobnih trikotnikov.
Poglejmo na Sliki31 vidni nasprotni par (5, 4) (m
=5, n = 4). Na sliki vidimo tri trikotnike, z osnovnicami na vertikali
0 in 1 ali blizu nje, vrhi trikotnikov pa so v točkah 5, 20 in 16. Trikotniki
so si pododobni. Prva dva prinašata relacijo u/md
v/n
in mv - nu = 1, kjer je v = 1 (korak od 0 do 5) in u
= 1 (korak od 1 do 5). V tem primeru je d manjši od 1/2, kot je zahtevano.
Zadnja dva trikotnika dajeta relacijo mv - nu = - 1 in v/n
d
u/m,
kjer je v = 3 (korak od 1 do 16) in u = 4. V tem primeru pa d
ni manjši od 1/2.
Če je par (m, n) viden, potem sta para (m + n, n) in (m, n + m) razširitev para (m, n). Razširitev lahko ni več vidna, ker lahko točka m + n pade iz pasa S, med oblikovanjem osnovnega paralelograma 0, m, n. Na primer, na Sliki 31 je par (5, 19) viden, vendar razširitvi (5, 24) in (24, 19) nista več vidni. Isto lahko rečemo za krčitev para (m, n). Krčitev para (m, n) je par (m - n, n) za m > n in par (m, n - m) za m < n. Nadalje, par (m, n) je lahko nasproten, vendar krčitev lahko ni več nasprotna. Primer vidimo na Sliki 31 krčitev (4, 15) od para (19, 15).
Izrek
3.
(1) Če je (m, n), m > n, viden, potem je vidna tudi
njegova krčitev in (md) - (nd) = ((m - n)d);
(2) Če je (m, n), m > n, viden in nasproten, potem je
njegova krčitev vidna in nasprotna in velja
mDn + nDm = 1, Dm + Dn
= Dm - n. Pri tem je Dx = |xd - (xd)|,
x = n, m, m - n;
(3) Če je (m, n), viden in nasproten, potem sta obe njegovi razširitvi
vidni, vsaj ena je tudi nasprotna, in velja Dm - n = |Dm
- Dn|.
Poglejmo si take mrežne točke m, n, da so pari (m, n) vidni in nasprotni. Na vsakem koncu vertikalne osi skozi točko 0 povežemo točke z neskončnimi lomljenimi črtami (glej Sliko 34). Če je d iracionalno število, potem med dvema črtama ni nobene mrežne točke razen 0. Relacije v Izreku 3 nam kažejo, da se lomljene črte približujejo vertikalni osi. Mrežne točke na teh črtah so sosedne točke vertikalne osi. Te točke ustrezajo točkam kvadratne mreže na premicah, ki se približujejo premici y = dx z divergenco d. Z predpostavko bratov Bravais, ki zahteva menjavo sosednih točk dobimo Izrek 4.
Izrek
4.
Če je d iracionalno število, manjše od 1/2, če je par (m, n),
m > n, viden in nasproten in če se sosedne točke od n in m
vertikalne osi neomejeno izmenjujejo vsaka na svojo stran ob vertikalni osi,
potem je d = [t(md) + (nd)]/(
t m + n).
Izrek
5.
Za poljubno zaporedje ulomkov (kd)/k, kjer oznaka (x)
pomeni najbližje celo število k x, k = 1, 2, 3, …, zgrajeno kot
v računskem algoritmu in za poljubni d,
so zaporedni vidni pari (mi, mi
+ 1), i = 1, 2, 3, …, k (zaporedni imenovalci v vsoti) ,
kjer je x prva mrežna točka, za točko 1, na drugi strani vertikalne osi
glede na točko 1.
/\ /\ /\ /\
|| || || ||