Iz osnovnega izreka filotakse lahko izpeljemo štiri algoritme, ki nam omogočajo določitev intervala za d iz vidnega nasprotujočega parastihijskega para (m, n) in vidne nasprotne parastihijske pare iz vrednosti d.
Računski algoritem: vsi vidni pari so določeni s podano
divergenco d.
Diofantski algoritem: s podanim poljubnim vidnim nasprotnim
parom dobimo interval za d.
Krčitveni algoritem: s podanim poljubnim vidnim nasprotnim
parom, sestavljenim iz sekundarnih števil zaporedja normalne in posebne filotakse,
dobimo interval za d.
Grafični algoritem: vidni par je določen s podano divergenco
d.
Vzemimo zopet divergenco d =t - 2, ko se da elegantno in enostavno izpeljati vidne nasprotne parastihijske pare s kalkulatorjem.
Tabela 2: Primeri limitnih divergentnih kotov, katerim ustrezajo vzorci normalne in posebne filotakse
Računski algoritem (za določitev
vidnih nasprotnih parastihijskih parov iz vrednosti divergentnega kota).
Predpostavimo, da je kot pravilne mreže d =t
- 2. Za zaporedne vrednosti k = 1, 2, 3, 4, …, določimo zaporedje
A, ki vsebuje ulomke (kd)/k, kjer oznaka (x)
pomeni najbližje celo število k x . Če je kd = I + 0.5,
kjer je I celo število, potem vzamemo oba I in I +1. Zaporedje
A do k = 21 je (če se ulomek ponovi, vzamemo le prvo pojavitev):
Poglejmo si celo število k, ki nam da rezultat (kd) = 1. Prvo
tako število je k = 2, 2-krat d je približno 0.76 in (0.76) je
enako 1. Sedaj razvrstimo zgornje ulomke v naraščajoče zaporedje, z zaporednim
vstavljanjem med 0/1 in (kd)/k = 1/2. Upoštevamo, da je naslednji
ulomek (v našem primeru 1/3 potem 2/5, itd.) Fareyeva vsota prejšnjih dveh.
[Fareyeva vsota ulomkov p / q in s
/ t je (p + s) / (q + t)]. Na primer imamo1/3 = (0 +1)/(1
+ 2) in 2/5 = (1 + 1)/(3 +2), itd. Fareyeva vsota ulomkov je vedno med ulomkoma.
Z nadaljevanjem postopka dobimo:
Zaporedna imenovalca m in n dveh ulomkov, na obeh straneh vzdolžnega odseka predstavljata vrednost d. Ob vsakem koraku v postopku nam dasta vidni nasprotni par (m,n). V našem primeru so vidni nasprotni pari: (1, 2), (3, 2), (3, 5), (8, 5), (8, 13), in (21, 13). Zaporedni imenovalci nam ob vsakem koraku dajo vidne pare. Če je d racionalno število p/q, sta dve zaporedji vidnih nasprotnih parov, točka p/g je na vertikalni osi. Če je d iracionalno število, kot v našem primeru, potem je le eno zaporedje vidnih nasprotnih parov, vsak par v zaporedju je zgrajen iz zaporednih Fibonaccijevih števil.
Krčitveni algoritem (določitev intervala za divergenco
iz vidnih nasprotnih parastihijskih parov v primeru normalne in posebne filotakse).
Imenujmo krčitev vidnega nasprotnega parastihijskega para (m, n), par
(m, n - m) če je m < n, in par (m - n, n) če
je m > n. Krčitev vidnega nasprotnega parastihijskega para
je viden nasproten parastihijski par.
Predpostavimo, da je par (19, 31) viden nasproten parastihijski par. Iščemo interval, katerih končni točki imata imenovalca 19 in 31. Vzemimo zaporedne krčitve tega para tako, da pridemo do para tipa J(t, t + 1) ali (2t + 1, 2t + 3). Poglejmo si postopek:
Opazimo, da sta sekundarni števili danega para zaporedna člena v zaporedju
posebne filotakse <2, 5, 7, 12, 19, 31, …>, par (7, 5) ima obliko (2t
+ 3, 2t + 1) za t = 2. Napišemo ustrezen interval, ki je za ta
primer [t/(2t +1), (t +1)/(2t +3)] = [2/5, 3/7]
in je določen po izreku filotakse, nato gremo nazaj
s Fareyevimi vsotami končnih točk. Dobimo, da je divergentni kot znotraj intervala
[13/31, 8/19], to je med 150,97° in 151,58°. Kota obdajata limitno divergenco
posebne filotakse za t = 2, ki ima vrednost 151.14° (glej Tabela
2).
V primeru, da sekundarni števili vidnega nasprotnega para vodita do skrčitve
J(t, t + 1), vzamemo Fareyeve vsote tako kot prej, le da začnemo z intervalom
[1/J(t + 1), /Jt], ki je podan z izrekom v normalni filotaksi.
Naj bo m = t in n = 1 v Izreku
4, (nd) = 0, (md) = 1, d = 1/(t +t-1), dobili smo divergenco normalne filotakse.
Če je t =2, se v sistemu pokaže Fibonaccijevo zaporedje.
Vzemimo za n = 2 in m = 2t +1, potem dobimo (nd) = 1, Dn
= 2d - 1, Dm = t - d(2t + 1) (Izrek
3), in (md) = t. Dobimo divergenco posebne
filotakse.
Posledica dokaza Izreka 1 je enostaven algoritem
za določanje vidnih parov in ne samo vidnih nasprotnih parov iz podzaporedja
A od F(N), določenega z d. Izrek
2 nam da enostaven algoritem za določanje intervalov za d iz vidnih nasprotnih
parov. Predstavljena sta že dva algoritma, sledita še dva.
Grafični algoritem (za določitev vidnih parastihijskih
parov iz računalniške slike pasa S, ki se ujema z d in poljubnim r).
Pogledamo si prvih N točk pasa S, z začetkom žarka v 0 in smo
pozorni na zaporedne točke, ki jih srečamo. Vidne pare (m, n), m,
n N, dobimo z poljubnima dvema zaporednima točkama. Krčitve takih parov,
so tudi vidne (Izrek 3). Ni nujno, da uporabimo
krčitve; lahko nadaljujemo z sledenjem žarka iz 0 na pasu S, za N
= 2, 3, 4, … .
Poglejmo si Sliko 32 za N = 29 in d = 100°
ali 5/18 ter s sledenjem žarku iz 0 dobimo sledeče zaporedne točke:
1 5 9 4 27 23 19 15 26 11 29 18 25 7 24 17 10 13 3 2.
Vidni pari do m, n = 19 so (1, 5), (5, 9), (9, 4),…, (10, 13), (13, 3),
(3, 2) in vse krčitve teh parov. Para (29, 18) in (18, 25) sta vidna in nasprotna,
skupaj s svojimi krčitvami, ko so (11,18), (18, 7), (11,7), (4, 7), (4, 3),
(1,3), (1, 2). Na Sliki vidimo, da je med krčitvami najbolj opazen par (4, 3).
Točka 9 je taka, da je (9d)/9 2/9 in 1/3. Po izreku
1 je (9d) = 2, para (5, 9) in (9, 4) sta vidna. V primeru (9d)
= 3, 9 ni vidna. Upoštevajmo, da so točke 9, 27, 45, … na desni strani pasu
S. Za d je 1/(3 +t -1), je iracionalna
vrednost med 8/29 in 5/18, para (18, 25) in (18, 7) pa nista več nasprotna in
imamo le eno zaporedje vidnih nasprotnih parov.
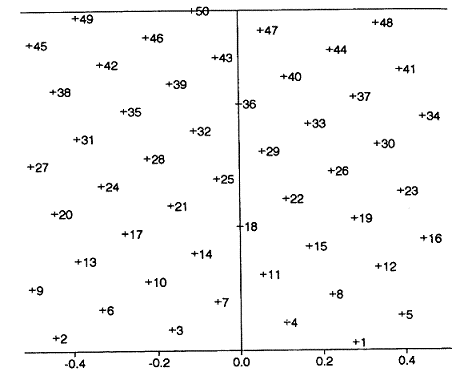
Slika 32: Cilindrična predstavitev mreže točk
Diofantski algoritem (določitev intervala
za divergentni kot d iz podanega vidnega nasprotnega para (m, n)).
Algoritem rešuje diofantsko enačbo |nu - mv| = 1 iz osnovnega
izreka filotakse. Na primer vidni par (29, 18), ima možne rešitve za u
in v: u = 29p± 8 in v = 18p±
5, kjer je p poljubno celo število. Če upoštevamo 0 < u <
29 in 0 < v < 18, potem dobimo p = 1 ( kar nam da u
= 21 in v = 13) ali p = 0 (kar nam da u = 8 in v
= 5), vendar le za p = 0 je divergenca manjša od 1/2 , tako da je interval
za d po Izreku [8/29, 5/18].
Da ponazorimo Izrek 5 vzemimo četrto vrsto ulomkov
za d =t - 2, podan z računskim
algoritmom. Imamo k = 4 in vidni pari v tej vrsti so (1, 3), (3,
5), (5, 7), (7, 2), kar nam da (1/3) + (1/15) + (1/35) + (1/14) = 1/2 [x
=2 za d večji od 90°, in x = n za d med 180°/n
in 180°/(n - 1)].
/\ /\ /\ /\
|| || || ||