FORMULA PRIBLIŽKOV BRATOV BRAVAIS

Valjasta mreža
Izpeljava formule

Valjasta mreža
Brata L. Bravais in A. Bravais (1837), sta intuitivno našla formulo za približek divergentnega kota. Formula za posamezne ulomke filotakse je d(tu + sv)/(tm + sn), kjer so u, v, m, in n cela števila, podana v splošni obliki temeljnega izreka in t ter s celi števili, pridobljeni iz mreže bratov Bravais za preučevanje filotakse. Definirali bomo to valjasto mrežo.
Na Sliki 33 je narisan smrekov storž, ki si ga lahko predstavljamo kot valj. Površina valja je oblikovana z črto, imenovano generator, le ta se paralelno pomika proti sebi v tridimenzionalnem prostoru vzdolž oboda kroga, ki je osnova tega valja. Valjast storž prerežemo vzdolž generatorja, ki ga predstavlja os Y in premica X na Sliki 34, razvijemo jo v ravnino, kar nam da valjast prikaz storža.

Slika 33: Smrekov storž

Slika 34: Cilindrična predstavitev mreže bratov Bravais

V tej predstavitvi so središča lusk storža predstavljena kot točke. Predvidevamo, da je mreža normalna, da je koordinata (d, r) točke 1 dovolj za postavitev vseh mrežnih točk. Divergentni kot d je konstanten in je enak vodoravni razdalji med poljubnima dvema zaporednima točkama na rodovni spirali. Parameter r je dvig oziroma naklon in se ujema z medrastnim kvocientom R v središčni predstavitvi. Enak je navpični razdalji med dvema zaporednima točkama n in n + 1 na rodovni spirali. Na valjasti mreži so poganjki enakomerno porazdeljeni znotraj navpičnega pasu širine 1, in parastihije so predstavljene kot vzporedne, enako oddaljene premice. Koordinata točke n je (nd - (nd), nr), kjer je (x) najbližje celo število števila x. Abscisa n se imenuje sekundarna divergenca točke n in njena vrednost je znotraj zaprtega intervala [- 0.5, 0.5 ]. V tem prikazu je parastihijski par (m, n) nasproten, če sta točki m in n na nasprotnih straneh osi Y. V navpičnem pasu točk z absciso med -1/2 in 1/2, je par (m, n) viden, če je trikotnik 0, m in n ne vsebuje druge točke na ali v trikotniku. Ta definicija je ekvivalentna definiciji, ki je bila podana na začetku. Točki m in n, ki sta najbližje koordinatnemu izhodišču, določata jasen par (m, n). Par je viden in nasproten.

Izpeljava formule
Na storžu, kot je na Sliki 33, ne moremo videti notranjih točk, kjer so pritrjene luske, kot vidimo vedno rastišče lista na steblu. Vendar vseeno lahko določimo ulomek filotakse na naslednji način. Izberemo si lusko na dnu storža in jo označimo z 0. Potem označimo še ostale luske storža po izreku bratov Bravais. Storž ima (8, 5) dotikajoč se parastihijski par, m = 8 in n = 5. Zaporedne luske na 8-parastihiji se razlikujejo za 8 in na 5-parastihiji za 5. Da dobimo ulomek filotakse, moramo preiti iz luske 0 na drugo lusko, ki je priblžno nad 0 glede na os storža, to je luska 21.
Zaradi boljše predstave se poglejmo Sliko 34, ki prikazuje parastihijski par (8, 5). Da bi dosegli na primer lusko 21, moramo iti skozi tm + sn ( = 21) lusk, 0 izvzamemo, in naredimo ((tm + sn)d) obratov okoli storža (valja), kjer zunanji oklepaji pomenijo najbližje celo število številu (tm + sn)d. V primeru luske 21 imamo t = 2 in s = 1. Na Sliki vidimo, da moramo narediti s = 1 korak v smeri 5-parastihij, od 0 do 5, in t = 2 koraka v smeri 8-parastihij, od 5 do 13 ter od 13 do 21, da pridemo od 0 do 21. Splošneje sledi, da je pridobljeni ulomek filotakse ((tm + sn)d)/( tm + sn). Vendar po temeljnem izreku je d med u/m in v/n, tako da je ((tm + sn)d) = (tmd + snd) 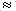(tm (u/m) + sn(v/n) = (tu + sv) = (tu + sv). Tako smo dobili formulo za približek.
Znamo določiti u in v iz diofantskega algoritma ali iz krčitvenega algoritma, začenši z relacijo mv - nu = 8v - 5u = 1 iz para (8, 5). Na Sliki 34 vidimo, da je v = 2 in u = 3. Upoštevajmo, da je mv - nu = 1 (glej temeljni izrek filotakse), če je 1 iz te enačbe luska številka 1, potem vidimo, da gremo od 0 do 1, v = 2 koraka moramo narediti v smeri 8-parastihij in u = 3 korake v smeri 5-parastihij. Tu je očitno še ena pot od 0 do 1, ki da v = 3 in u = 5, potem je u/m = 5/8 in v/n = 3/5, ki pa sta večja ulomka od 1/2, zato ta divergentni kot ne more biti med tema dvema ulomkoma, kakor to zahteva izrek. Končni približek, podan s formulo, je (3t + 2s)/(8t + 5s) = 8/21, to je vrednost znotraj intervala [3/8, 2/5] po Adlerjevem izreku za par (8, 5). Če bi vzeli točko 34 namesto 21, bi dobili približek 13/34 (t = 3, s = 2).

/\ /\ /\ /\
|| || || ||