SINUSNI

SINUSNI

SINUSNI IZREK

A

B

C

s

s

s

a

b

c

a

b

c

S

R

R

R

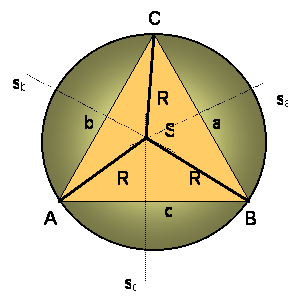Načrtaj raznostranični ostrokotni trikotnik ABC s stranicami a, b, c . Očrtaj mu krog!

Zveži S - središče trikotniku očrtanega kroga - z vsemi oglišči A, B IN C.

Tako je SA = SB = SC = R

R - polmer trikotniku očrtanega kroga

Trikotniki ABS, BCS in CAS so enakokraki trikotniki.

Oglej si enega od njih., npr trikotnik ABS!

C

A

B

S

R

a

b

c

c/2

M

R

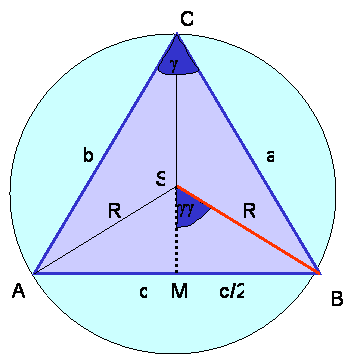Višina SM,na stranico AB , razdeli središčni kot a v dva enaka kota g.

V pravokotnem trikotniku AMS je:

sin g= (c/2)/R

c/2 = R . sin g

c = 2 . R . sin g

Na isti način bi izpeljal iz trikotnikov

BCS in CAS :

a = 2R . sin a

b = 2R . sin b

2R - premer kroga

Izpeljal si povezavo med stranico, njej naprotnim kotom in polmerom očrtanega kroga.

Stranico raznostraničnega trikotnika izračunaš tako, da premer očrtanega kroga pomnožiš s sinusom kota, ki je tej stranici nasproten.

a = 2R . sin a b = 2R . sinb c = 2R . sin g

Iz dobljenih obrazcev lahko izpelješ sinusni izrek, če zapišeš razmerja med stranicami:

a : b =.....(krajšaš z 2r)

a : c =

(Zapišeš še lahko več razmerij!)

a : b : c = sin a : sin b : sin g

To pa je sinusni izrek, ki se glasi:

Stranice raznostraničnega trikotnika so v enakem razmerju kakor sinusi naprotnih kotov

a : b : c = sin a : sin b : sin g

P R I M E R I :

Po sinusnem izreku razrešuješ trikotnik, če je:

a)znana ena stranica in dva kota

1. Reši trikotnik s podatki c = 8cm, a = 34⁰ 18' , b=62⁰ 39'

A

B

C

c

Izračunati moraš ostale osnovne trikotnikove sestavine, to sta še dve stranici a in b in trtetji kot g.

Iz a + b + g =180⁰ sledi: Skica:

g =180⁰- (a + b )

g= 180⁰ -(34⁰ 18' + 62⁰ 57')

g= 180⁰ – 96⁰ 57'

g = 83⁰ 3'

Upoštevaj, da je produkt zunanjih členov sorazmerja enak produktu notranjih členov

Iz a : c = sin a : sin g in b : c = sin b : sin g dobiš:

a . sin g = c . sin a (Deli s sin g!) in b . sin g= c . sin (Deli s sin g!)

a = c . sin a /sin g b = c . sin b / sin g

Vstavi dane podatke in opravi računske operacije:

a = 8 . sin 34⁰ 18' / sin 83⁰ 3' b = 8 . sin 62⁰ 39' / sin 83⁰ 3'

a = 8 . 0,56353 / 0,99266 b = 8 . 0,88822 / 0,99266

a = 4,54 = 4,5cm b = 7,15 = 7,2

a = 4,5cm b = 7,2cm

Sedaj poznaš vse trikotnikove osnovne sestavine; vse stranice in vse kote.

b) znani sta dve stranici in kot, ki leži eni od njih nasproti.

1. Reši trikotnik s podatki a = 10cm, b = 8cm, a = 48º 13'

A

B

C

a

b

Skica:

a : b= sin a : sin b

a . sin b = b . sin a /a

sin b = b . sin a /a

sin b = 8 . sin 48º13' / 10 = 8 . 0,74567/10 = 0,59654

sin b = 0,59654

b = 36º37'

Kot g dobiš iz obrazca: a + b + g = 180º

g = 180º - (a + b)

g = 180º- ( 48º13' + 36º37')= 180º - 84º50' = 95º10'

g= 95º10'

Tudi stranico c izračunaš po sinusnem izreku:

c : a = sin g: sin a

c =

c = 13,35cm

c = 13,4cm