PITAGOROV
Home Up KOSINUSNI SINUSNI VIŠINSKI KATETNI PITAGOROV

 

 

PITAGOROV IZREK

 PITAGOROV IZREK VELJA V PRAVOKOTNEM TRIKOTNIKU.

 c - HIPOTENUZA ( stranica nasproti pravemu kotu- najdaljša stranica pravokotnega trikotnika)

a, b - KATETI  ( stranici, priležni pravemu kotu)

 PITAGOROV IZREK

 

V PRAVOKOTNEM TRIKOTNIKU JE KVADRAT NAD  HIPOTENUZO ENAK VSOTI KVADRATOV NAD KATETAMA.

 c – hipotenuza

c2 – kvadrat nad hipotenuzo c

a - kateta

a2 – kvadrat nad kateto a

b -kateta

b2 – kvadrat nad kateto b

 

 

 

   

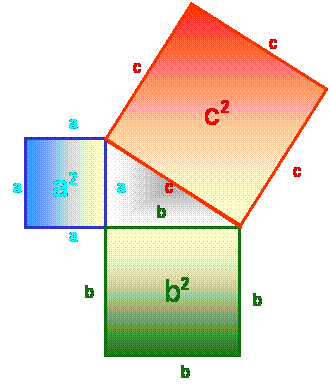
a2  +  b2  =  c2

DOKAZ:

b

c

a

a

a

b

b

c

c

c

c

2
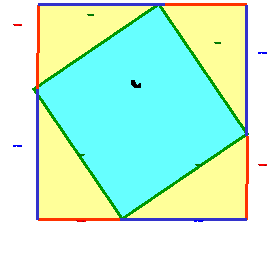Imaš kvadrat s stranico c včrtan kvardatu s stranico a + b :

 

Ploščina kvadrata s stranico a + b je :  S = (a + b)2  = a2 + 2ab + b2

Ploščina tega kvadrata je enaka  vsoti ploščin kvadrata s stranico c

 in štirih pravokotnih trikotnikov s katetama a in b.

 

S = c2+ 4. a . b/2 = c2 + 2. a . b             

Zapiši enakost:

(a + b)2 = c2 + 2. a . b

a2 + 2. a . b + b2  = c2 + 2 . a . b  /Odštej 2ab!

a2 + b2 = c2                              

Dokazal si Pitagorov izrek.

P R I M E R I

 1.     Izračunaj kateto a  pravokotnega trikotnika, če merita kateta b = 2cm in hipotenuza c =12cm!

 Zapiši Pitagorov izrek in vstavi dane podatke:

a

b

c

A

B

C

 a2 + b2 = c2                               Skica:

a2 + 22  = 122

a2 + 4  = 144

a2 = 144 - 4 = 140

a =

a = 11,83 cm

 Stranica a = 11,83cm

 

2. Na tleh 10 m stran od smreke je pikapolonica. Vrh smreke je od nje oddaljen 11m. Kako visoka je smreka?

 Nariši skico:               IBCI - hipotenuza

                                    IABI,IACI - kateti                                                 11m  

                                    IACI - višina smreke

Uporabi Pitagorov izrek:                                                                      

IABI 2+ IACI2 = IBCI2

102 + IACI2 =112                                                                                              10m

IACI2= 112 – 102 = 21

IACI =  = 4,583 m                                                                 

Smreka je visoka približno 4,538 metrov.

 

 3. V enakokrakem trikotniku meri osnovnica 2dm, krak pa 26cm! Izračunaj višino na osnovnico!

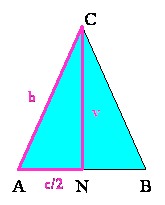
 Skica:    Višina enkokrakega trikotnika razdeli                             

               enakokraki trikotnik v dva skladna

               pravokotna trikotnika ANC in NBC.

 Zapiši Pitagorov izrek:   

                      v2 = b2 - (c/2)2

                      v2 = 262 – 102 = 576 v == 24cm

                      v = 24cm

 Višina enakokrakega trikotnika meri 24cm.

                        

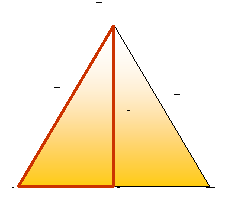
4. Dan je enakostranični trikotnik s stranico a. Izrazi višino enakostraničnega trikotnika s stranico a!

 Višina enakostraničnega trikotnika razdeli                IACI- hipotenuza a

 enakostranični trikotnik v dva skladna                       IANI = a/2 -kateta

 pravokotna trikotnika.                                                INCI- kateta = višina  v

A

B

C

v

a/2

a

a

N
 Zapiši Pitagorov izrek:

                     v2 = a - (a/2)

                     v2 = a2 - a2/4

                     v2 = 4a2/4 – a2/4

                     v2 = 3a2/4     Delno koreni!

                     v = =

v =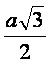

 Višina enakostraničnega trikotnika