KATETNI (EVKLIDOV) IZREK
KVADRAT NAD KATETO PRAVOKOTNEGA TRIKOTNIKA JE PLOŠČINSKO ENAK PRAVOKOTNIKU, KI IMA ENO STRANICO ENAKO HIPOTENUZI , DRUGA PA JE ENAKA ODSEKU NA HIPOTENUZI, KI PRIPADA TEJ KATETI.
|
a |
|
a |
|
a |
|
a |
|
a |
|
b |
|
b |
|
b |
|
b |
|
a |
|
b |
|
b |
|
a |
|
a |
|
b |
|
. |
|
. |
|
1 |
|
1 |
|
c |
|
c |
|
c |
|
2 |
|
2 |
|
c |
|
c |
|
1 |
|
1 |
|
1 |
|
1 |
a
- kateta
a1 – pripadajoči odsek na hipotenuzi c
b – kateta
b1 – pripadajoči odsek na hipotenuzi c
c = a1 + b1
DOKAZ:
Imaš pravokotni trikotnik ABC
s hipotenuzo c in višino v.
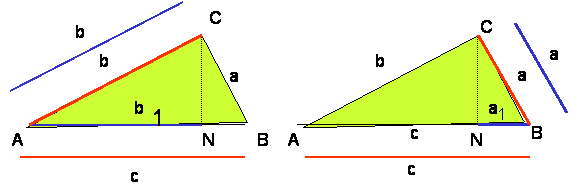Slika:
b1 - pravokotna projekcija katete b na c a1 - pravokotna projekcija katete a na c
(odsek b1 pripada kateti b) (odsek a1 pripada kateti a)
Trikotnika ABC in ANC sta podobna: Trikotnika ABC in NBC sta podobna:
ABC
~
NBC ABC
~
ANC
Velja: b : b1 = c : b Velja: a : a1 = c : a
b2 = b1 . c a2 = a1 . c
a2 = a1 . c b2 = b1 . c
P R I M E R I:
1. Izračunaj hipotenuzo pravokotnega trikotnika ABC s podatki a = 10cm
in a1= 6cm!
Zapiši Evklidov izrek in izrazi hipotenuzo c:
a2 = a1 . c
c = a2/a1
c = 102/6
c = 100/6
c = 16,6 cm
Hipotenuza meri trikotnika 16,6cm
2. Izračunaj hipotenuzo in kateti pravokotnega trikotnika, če merita pravokotni projekciji katet na hipotenuzo a1 = 3,8cm in b1= 4,2cm!
|
C |
|
A |
|
b |
|
c |
|
a |
|
B |
|
b |
|
a |
|
|
|
|
|
1 |
|
1 |
Zapiši Evklidov izrek:
Zapiši Evklidov izrek:
a2 = a1 . c b2 = b1 . c
a2 = 3,8 . 8 b2 = 4,2 . 8
a2 = 30,8 b2 = 33,6
a = 
b =
a = 5,53 cm b = 5,8 cm
Hipotenuza pravokotnega trikotnika ABC je
c = a1 + b1
c = 3,8 + 4,2
c = 8cm
Hipotenuza meri 8cm , kateti pa 5,53 cm in 5,8 cm.