KOSINUSNI
Home Up KOSINUSNI SINUSNI VIŠINSKI KATETNI PITAGOROV

 

 

KOSINUSNI IZREK

 

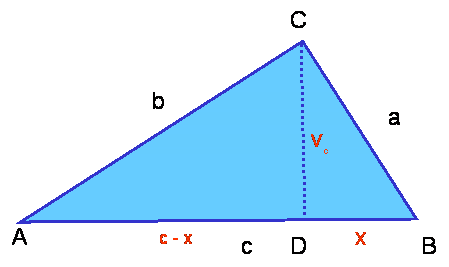
V raznostraničnem trikotniku ABC  načrtaj          

višino v = CD, ki razdeli stranico c v dva dela:

AD = x in BD = c - x     

V pravokotnem trikotniku ADC je po Pitagorovem izreku :

v= b- (c – x)2

 V pravokotnem trikotniku DBC

pa je po istem izreku:

v= a-  x2

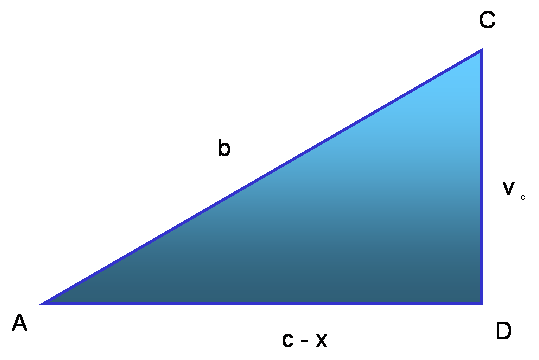
 Izenačimo oba izraza, ki smo ju našli za v:

a2 -  x2  =  b2 – (c – x)2 

a2 - x2 = b2 - (c2 -2cx + x2)

a2 - x2 = b2 - c2 +2cx - x2

a2 = b2 - c2 + 2cx

a2 + c2 - 2cx = b2

b2 = a2 + c2 - 2cx

Neznani odsek x izrazimo s stranico a in s kotom b

cos b =

x = a . cos b

 Zato je:

 b= a+ c- 2 . a . c . cos b

 Če bi načrtal namesto vvišino va ali vb bi lahko izpeljal

 enako zvezo med stranicami in enim kotom :

 a2 = b2 + c2 – 2.b .c . cos a

c2 = a2 + b2 – 2. a. b . cos g

 Vsi trije obrazci skupaj izražajo kosinusni izrek, ki se glasi:

 

Kvadrat stranice je enak vsoti kvadratov drugih dveh stranic, zmanjšani za dvojni produkt teh dveh stanic s kosinusom kota, ki ga ti dve stranici oklepata.

 

a = b + c - 2 . b . c . cos a

b = a + c - 2 . a . c . cos b

c = a + b - 2 . a .b . cos g

  

P R I M E R I :

 a) Znani sta dve stranici in kot, ki ga oklepata:

1. Reši trikotnik s podatki a = 7m, b = 5,5m, g = 54º31'

A

B

C

a

b
c = ?  a = ? , b = ?                       Skica:

 Uporabi kosinusni izrek :

c2 = a2 + b2 – 2.a.b.cos g

c2 = 72 + 5,52 - 2.7.5,5.cos 54º31'

c2 = 49+30,25 - 77.0,58046

c2= 34,5548

c = =5,878=5,88

c= 5,88m

Kot  a bi lahko izračunal po sinusnem izreku sin a : sin g = a : c !

Izračunal ga boš iz kosinusnega izreka:

a2 = b2 + c2 – 2.b.c.cos a

a2 - b2 - c2 = - 2bc.cos a/(-1)

b2 + c2 - a2 = 2bc.cos a/ delimo z 2bc

cos a = 

cos a =  

cos a = 0,24466        

a = 75º50'

 

Kot  b dobiš iz obrazca za vsoto kotov v triktniku.

b = 1800 – (a + g)

  

b) Znane so vse tri stranice trikotnika:

A

B

C

a

b

c
1. Reši trikotnik s podatki a = 95cm, b = 102cm, c = 120cm

a, b, g = ?                                                                            Skica:

Iz  a2 = b2 + c2 – 2. b . c . cos a dobiš cos a =

Iz b2 = a2 + c2 – 2. a . c . cos  b dobiš cos b =

iz c2 =a2 + b2 – 2. a. b . cos g dobiš cos g =

 

cos

 a = 49052’

Izračunaj še ostala kota.

cos  b = …………….                                            

b = …………………

cos g  =…………….

g  = ……………….