PODOBNOST TRIKOTNIKOV
Home Up KOTNE FUNKCIJE IZREKI PLOŠČINA TRIKOTNIKA PODOBNOST TRIKOTNIKOV SKLADNOST TRIKOTNIKOV ZNAMENITE TOCKE VRSTE TRIKOTNIKOV OSNOVNI POJMI

 

 

 

 POJEM PODOBNOSTI

 V vsakdanjem življenju ima izraz “podoben” ralične pomene. Osebe ali stvari so lahko med seboj bolj ali manj podobne.V matematiki moramo pojem podoben natančno določiti. Na sliki so načrtani podobni krogi, kvadrati, pravilni petkotniki itd.

 

 

 

 

 

 

 

  Podobna lika nastaneta drug iz drugega tako, da se pri tem ohranijo vsa razmerja ustrezno prirejenih stranic in velikosti vseh medsebojno prirejenih kotov.

 

 

 

 

 

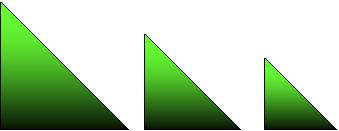
 Narisani trikotniki imajo enake kote in stranice narisane v izbranem merilu. Merilo, to je razmerje stranic k, pove, ali si lik povečal (k > 0) ali zmanjšal (k <  0 < 1) ali pa si ga pustil nespremenjenega (k = 1).

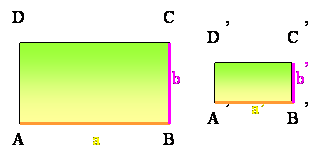
 Podobna pravokotnika ABCD IN A’B’C’D’ na sliki sta narisana v razmerju 2 : 1. To pomeni, da so stranice trikotnika A’B’C’D’ dvakrat daljše.

 

A

B

C

D

A

B

C

D

,

,

,

,

a

a

b

b

,

,

 

      ABCD ~      A’B’C’D’

~ znak za podobnost

 k = 2

 Podobna lika imata enako razmerje vseh ustrezno prirejenih stranic in enake kote. Merilo podobnih likov k imenujemo podobnostni koeficient.

 

 PODOBNOST TRIKOTNIKOV

 Trikotniki imajo posebno vlogo pri obravnavanju podobnosti.

 Koti trikotnika in podobnost

B

C

C

C

A

A

B

B
 

 

 

 

 

 

,,

,

,

,

,

,,
 
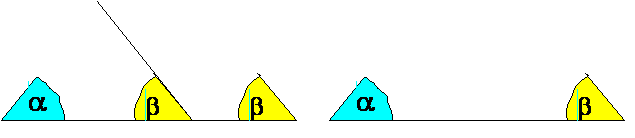
 Trikotnik ABC je preslikan tako, da je dolžina daljice AB’’ enaka dolžini A’B’.
AB’’ = A’B’. Ker še velja, da je a = a’ in  b = b’ sta trikotnika AB’’C’’ IN A’B’C’ skladna.
Iz tega sledi, da sta trikotnika ABC in A’B’C’ podobna.

 Trikotnika sta podobna, če se ujemata v dveh kotih.

 Ð a =Ð a’  ; Ð b = Ð b’  ;  Ð g = Ð g’

 

DA STA TRIKOTNIKA ABC IN A'B'C' PODOBNA PRAV TAKO ZAPIŠEŠ Z ZNAKOM

 ~.

 ~ znak za podobnost

Razmerja stranic in podobnost

 Trikotnik ABC preslikaj v merilu 1:2 v podoben trikotnik ABC. Stranice trikotnika ABC so a, b, c, stranice trikotnika pa so: a = 2a, b = 2b in c = 2c.

A

B

C

a

b

c

B

C

a

c

b

,

,

,

,

,

,

 

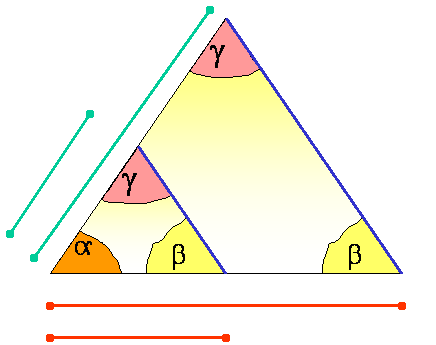
STRANICI TRIKOTNIKA, KI LEŽITA NASPROTI  ENAKIMA KOTOMA STA USTREZNO PRIREJENI IN JU

 IMENUJEMO ISTOLEŽNI ALI ENAKOLEŽNI STRANICI.

 

 

 

 

 

 

 

 

 

 Enakoležni stranici sta:

enakima kotoma g  in g’ nasproti ležita stranici c in c’

enakima kotoma b in b’ nasproti ležita stranici b in b’,

skupnemu kotu a nasproti ležita stranici a in a’.

 Trikotnika sta podobna, če so stranice enega od njih premo sorazmerne istoležnim stranicam drugega.

 Razmerje vsakega para istoležnih stranic podobnih trikotnikov je:

 ,   ,  

Torej je:

 

 

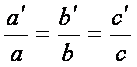
 Narisana imaš podobna trikotnika ABC in A’B’C’.

A

B

C

a

b

c

C

A

c

b

a

,

,

,

,

,

 

 

 

 

 

 

 Stranice izmeri (čim bolj natančno) in rezultate merjenja zapiši v tabelo in izračunaj razmerje med stranicami .(na eno decimalko natančno)

 

ISTOLEŽNI STRANICI

RAZMERJE MED ISTOLEŽNIMA STR.

KOLIČNIK

a =                a' =

a : a' =

k =

b =                b' =

b : b' =

k =

c =                c' =

c : c' =

k =

Izračunaj še ta razmerja:

 

RAZMERJE

KOLIČNIK

RAZMERJE

KOLIČNIK

a : b =

k =

a' : b’ =

k =

b : c =

k =

b' : c’=

k =

a : c =

k =

a' : c' =

k =

  

Ugotovitev: RAZMERJE KATERIHKOLI DVEH STRANIC ENEGA TRIKOTNIKA JE ENAKO RAZMERJU ENAKOLEŽNIH STRANIC DRUGEGA TRIKOTNIKA.

 Združi obe ugotovitvi:

 DVA TRIKOTNIKA STA SI PODOBNA, ČE SE UJEMATA V KOTIH IN V RAZMERJU PO DVEH ENAKOLEŽNIH STRANIC.

ZA PODOBNA TRIKOTNIKA S KOTI a, b, g  IN  a’, b’, g’  TER STRANICAMI a,  b,  c, in a',  b', c', VELJA:

 

a' = k . a    b' = k . b     c' = k . c

k  JE KOEFICIENT PODOBNOSTI.