OZNAČEVANJE TRIKOTNIKA
TRIKOTNIK JE RAVNINSKI LIK, KI GA DOLOČAJO TRI NEKOLINEARNE TOČKE.
Potrebno predznanje:
TRI TOČKE SO KOLINEARNE, ČE LEŽIJO NA ISTI PREMICI.
C
B
A
|
A |
|
B |
|
C |
|
c |
|
a |
|
b |
A, B IN C SO NEKOLINEARNE TOČKE.
PONOVIMO ZNANJE O TOČKI, PREMICI, DALJICI IN POLTRAKU.
TOČKA JE MESTO V PROSTORU. Označimo jo z velikimi tiskanimi črkami
A
B
PREMICA JE SESTAVLJENA IZ NESKONČNO VELIKEGA ŠTEVILA TOČK.
( Skozi dve različni točki poteka natanko ena premica). Označimo jo z malimi tiskanimi črkami.
A p B
RAVNINA JE NESKONČNO VELIKA RAVNA PLOSKEV.
p
|
A |
|
B |
|
C |
|
c |
|
a |
|
b |
A, B, C
- OGLIŠČA TRIKOTNIKA
a, b, c - STRANICE TRIKOTNIKA;
(Stranica je daljica.) AB = c, BC = a, AC = b
Nasproti oglišču A leži stranica a,
nasproti oglišču B leži stranica b,
nasproti oglišču C leži stranica c.
Točke A, B, C si sledijo v nasprotni smeri od urnega kazalca. (pozitivna orientacija)
ODNOSI MED STRANICAMI TRIKOTNIKA
V zvezek načrtaj trikotnike s podatki: a) c = 5cm, a = 3cm, b = 2cm.
b) c = 5cm, a = 3cm, b = 3cm
Kaj ugotoviš? c) c = 5cm, a = 3cm, b = 9cm
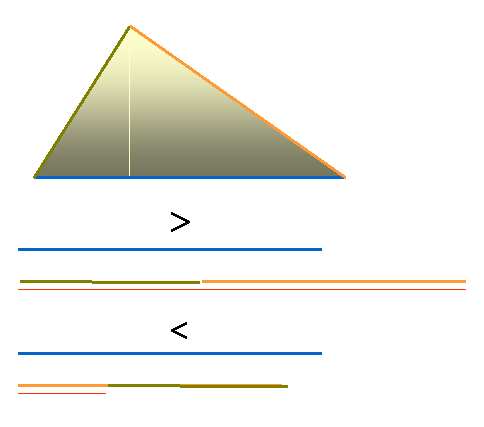
VSOTA DVEH STRANIC JE VEČJA OD DOLŽINE TRETJE STRANICE.
a + b > c
VELJA ŠE: b + c > a in a + c > b
ABSOLUTNA VREDNOST RAZLIKE DOLŽIN DVEH STRANIC JE MANJŠA OD DOLŽINE TRETJE STRANICE:
I a - b I < c
VELJA ŠE: I b – c I < a in I a – c I < b
PRIMERI :
V tabeli imaš dani stranici. Za tretjo stranico ugotovi in zapiši meje!
|
c = 3cm |
b = 9cm |
12cm < a < 6cm |
|
a =12,3cm |
b = 8,4cm |
< c < |
|
a = 4,5dm |
c = 3dm |
< b < |
|
= 2m |
c = 13dm |
< b < |
|
c = 2dm 4cm |
a = 6dm 7cm |
< b < |
|
A |
|
B |
|
C |
|
b |
|
c |
|
a |
|
a |
|
c |
|
a |
|
c |
|
b |
|
b |
|
A |
|
A |
|
B |
|
B |
|
A |
|
A |
|
C |
|
C |
|
B |
|
a |
|
b |
|
+ |
|
a |
|
b |
|
- |
|
c |
|
c |
|
a + b |
|
a - b |
Dopolni tabelo!
NOTRANJI IN ZUNANJI KOTI TRIKOTNIKA
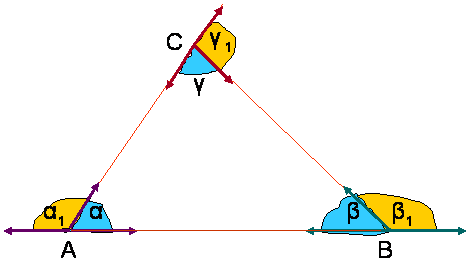
a, b, g - NOTRANJI KOTI
a1, b1, g1 - ZUNANJI KOTI
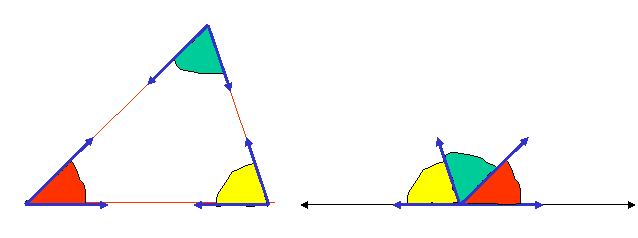
NOTRANJI KOTI VSOTA NOTRANJIH
KOTOV TRIKOTNIKA JE 1800.
Dokaz:
a
+
b
+
g
= 180 0
|
A |
|
B |
|
C |
|
V |
|
A |
|
B |
|
C |
|
1 |
|
1 |
|
1 |
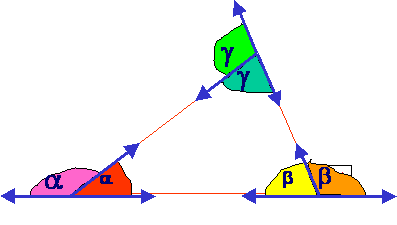ZUNANJI KOTI
VSOTA ZUNANJIH TRIKOTNIKOVIH
KOTOV JE ENAKA 3600.
a1 + b1 + g1 = 360 0
|
1 |
|
1 |
|
1 |
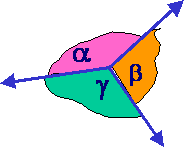
ZUNANJI KOTI SO SOKOTI NOTRANJIH TRIKOTNIKOVIH KOTOV.
ZUNANJI KOT JE ENAK VSOTI DVEH NOTRANJIH NEPRILEŽNIH KOTOV.
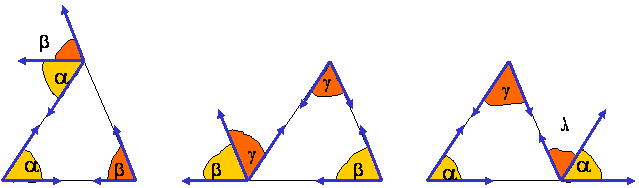a1 =
b
+
g
b1
=
a +
g
g1 =
a +
b
ODNOSI MED STRANICAMI IN KOTI TRIKOTNIK
|
A |
|
B |
|
C |
|
a |
|
b |
|
c |
|
A |
|
B |
|
C |
|
a |
|
b |
|
c |
V TRIKOTNIKU LEŽI VEČJI
STRANICI NASPROTI VEČJI KOT, MANJŠI STRANICI MANJŠI KOT, ENAKIM STRANICAM
NASPROTI ENAKI KOT IN OBRATNO, VEČJEMU KOTU NASPROTI LEŽI VEČJA STRANICA ITD.
a = b Û a = b a < b < c Û a < b < g
a > c Û a > g