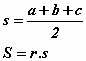OSNOVNI POJMI
Narisana sta dva pravokotna trikotnika s kotom a
= 60º! Prvega označi z A, B, in C., drugega pa z A1, B1 in C1. Ker imata oba trikotnika kot ob oglišču C in C1 pravi kot in enak kot ob oglišču A in A1, sta tudi kota v ogliščih B in B1 enaka.Slika:
|
C |
|
C |
|
A |
|
A |
|
B |
|
B |
|
a |
|
a |
|
b |
|
b |
|
c |
|
c |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
Izmeri stranice obeh trikotnikov in jih zapiši :
a = ………. a1 =……….
b = ………. b1 =……….
c = ………. c1 =……….
Stranici a in a1, b in b1 in c in c1 so pari enakoležnih stranic. Izračunaj količnike (razmerja) med naslednjimi stranicami trikotnika in jih primerjaj: (Izračunaj z osebnim računalnikom na eno decimalko natančno!)
a : c = ………. b : c = ………. a : b =……….
a1 : c1 = ………. b1 : c1 = ………. a1 : b1 =……….
Kaj si ugotovil? Vsi pravokotni trikotniki, ki jih sestaviš s tem kotom a so podobni in razmerja med stranicami sploh niso odvisna od tega kako velik je trikotnik (niso odvisna od dolžine stranic) temveč od tega, kako velik kot a si načrtal.( Če kot a spremeniš se vrednosti razmerij spremenijo! Poskusi s kotom a = 40º!)
RAZMERJA MED STRANICAMI PRAVOKOTNEGA TRIKOTNIKA SO ODVISNA OD VELIKOSTI KOTA a .
V MATEMATIKI "ODVISNO OD" IMENUJEMO FUNKCIJA.
RAZMERJA MED STRANICAMI PRAVOKOTNEGA TRIKOTNIKA SO FUNKCIJE KOTA a , ALI KOTNE FUNKCIJE.
KOTNE FUNKCIJE IMAJO SVOJA IMENA:
Poimenuj stranice pravokotnega trikotnika glede na lego kota a
a- kotu a nasprotna kateta
|
B |
|
C |
|
A |
|
a - nasprotna
kateta |
|
b - priležna
kateta |
|
c - hipotenuza |
b- kotu a priležna kateta
c - hipotenuza
a : c = a/c = 
=sin
a (sinus a )
b: c= b/c = 
= cos a
(kosinus a )
a: b = a/b = 
= tg a
(tangens a )
b : a = b/a = 
= ctg
a (kotangens a )
Ostali kotni funkciji sta še sekans (sec) in kosekans (cosec), ki jih pa ne boš uporabljal!
Če v obrazce vneseš poimenovanje stranic pravokotnega trikotnika dobiš sledeče definicije.:
DOBRO SI ZAPOMNI SLEDEČE DEFINICIJE, KAJTI UPORABLJAL JIH BOŠ SKORAJ PRI VSEH PREDMETIH, KI SO POVEZANI Z MATEMATIKO!!
SINUS JE RAZMERJE MED NASPROTNO KATETO (a) IN HIPOTENUZO (c).
KOSINUS JE RAZMERJE MED PRILEŽNO KATETO (b) IN HIPOTENUZO (c).
TANGENS JE RAZMERJE MED NASPROTNO KATETO (a) IN PRILEŽNO KATETO (b).
KOTANGENS JE RAZMERJE MED PRILEŽNO KATETO (b) IN NASPROTNO KATETO (a).
KOTNE FUNKCIJE SO KOT RAZMERJA DVEH STRANIC PRAVOKOTNEGA TRIKOTNIKA NEIMENOVANA ŠTEVILA.
Definicije za kotne funkcije si zapomni z besedami,da boš lahko določil(a) funkcije tudi v takem pravokotnem trikotniku, kjer stranice in koti ne bodo označeni na običajni način ( koti z alfa, beta, gama in stranice z a, b in c)
P R I M E R I:
1. Določi kotne funkcije kota j , ki ga v pravokotnem trikotniku s stranicami r, s in v oklepata kateta v in hipotenuza s!
Slika:
Najprej moraš vedeti:
|
r |
|
v |
|
s |
- kotu j priležna kateta je v,
- kotu j nasprotna kateta je r,
- hipotenuza je s
Zato je: sin j = nasprotna kateta/hipotenuza = r / s
cos j = priležna kateta/hipotenuza = v / s
tg j = nasprotna kateta/priležna kateta = r / v
ctg j = priležna kateta/nasprotna kateta = v / r
2. Izračunaj vrednosti kotnih funkcij za kota a in b v pravokotnem trikotniku s katetama a = 3,6cm in b = 4,8cm!
Obvezno nariši skico!
|
b |
|
a |
|
c |
Izračunaj najprej hipotenuzo c po
Pitagorovem izreku je:
c
= a
+
b
c
= 3,6
+ 4,8
c
= 12,96 + 2
3,04
c
= 36
c = 6cm
Zdaj določi kotne funkcije kota a :
sin a = a/c = 3,6/6 = 0,6
cos a = b/c = 4,8/6 =............. tg a = a/b = 3,6/4,8 =.............ctg a = b/a = 4,8/3,6 =...........................
Določi še kotne funkcije kota b :
sin b = b/c = 4,8/6 =......................cos b = a/c = 3,6/6 = 0,6 tg b = b/a = 4,8/3,6 =......................
ctg b = a/b = 3,6/4,8 =......................
Primerjaj rezultate v obeh primerih!
Gotovo si opazil(a), da je vrednost sinus kota a enaka vrednosti kosinusu kota b . Torej je: sin a = cos b = 0,6.
Zapiši še ostale enakosti!
.......................................... ...........................................
........................................... ...........................................
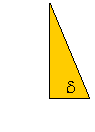
3. Načrtaj kot d , če je: a) tg d = 3 b)cos d = 3/4 !
a) Ker veš, da je tangens razmerje med nasprotno kateto in priležno kateto, načrtaj pravokotni trikotnik s katetami 3cm in 1cm saj je tg d = 3 = 3/1.
Kot, ki je nasproten kateti 3cm, je iskani kot d , saj mu je kateta 3cm nasprotna, kateta 1cm pa priležna.
b)Ker je kosinus razmerje med priležno kateto in hipotenuzo, nariši pravokotni trikotnik s hipotenuzo 4cm in z kateto 3cm. Kot, ki je priležen kateti 3cm, je iskani kot d .
Slika: a) Slika b)
|
1cm |
|
3cm |
|
4cm |
|
3cm |
Ali bi lahko dobil večjo sliko? (3 = 3/1 = 6/2 = 9/3) (3/4 = 6/8 = 12/16)
KOTNE FUNKCIJE KOMPLEMENTARNIH KOTOV
OSTRA KOTA V PRAVOKOTNEM TRIKOTNIKU STA KOMPLEMENTARNA, KER MERITA SKUPAJ 90º.
Iz a + b = 900 lahko izračunaš kot b tako:
b = 900 - aa =
20º Þ b = 900 - a Þ b = 90º - 20º Þ b = 70ºDoloči kotne funkcije za kota a in b v pravokotnem trikotniku ABC !
Slika:
|
b |
|
a |
|
c |
|
A |
|
B |
|
C |
sin a = a / c sin b =...../......
cos a =...../.......
cos b = a / ctg a = ...../...... tg b =...../......
ctg a =...../...... ctg b =...../......
Zapiši enakosti in namesto kota b zapiši b = 900 - a
sin a = cos b Þ sin a
= cos (90º - a )cos a = sin b Þ cos a
= sin (90º - a )tg a = ctg b Þ tg a
= ctg (90º - a )ctg a = tg b Þ ctg a
= tg (90º - a )P R I M E R I:
- sin 40º = cos ( 90º - 40º ) = cos 50º
- tg 21º = ctg ( 90º- 21º) = ctg 69º
3.
ctg 14º 38' = tg ( 90º - 14º 38' ) = tg 75º 22'4.
cos 72º 15' 43'' = sin ( 90º- 72º 15' 43'' ) = sin 17º 44' 17''
VREDNOSTI KOTNIH FUNKCIJ ZA KOTE 30º , 45º IN 60º.
KOTNE
FUNKCIJE KOTOV 30º IN 60º LAHKO IZPELJEŠ IZ PRAVOKOTNEGA TRIKOTNIKA, KI JE POLOVICA ENAKOSTRANIČNEGA TRIKOTNIKA.Na sliki je enakostraničnemu trikotniku narisana višina na stranico a.
Višino izrazi s stranico a! Še enkrat ponovi izpeljavo!
a = hipotenuza a/2 = kateta va = ?
Uporabi Pitagorov izrek:
v
= a
- (a/2)
v
= a
- 
v2 =
v
=
višina enakostraničnega trikotnika
1) za kot 30º velja:
= nasprotna
kateta, 
= priležna kateta, a =
hipotenuza
sin 30º =
cos 30º =
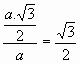
tg 30º =
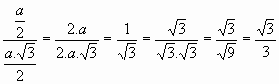
ctg 30º =
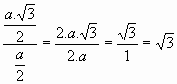
2) za kot 60º velja
= nasprotna
kateta , 
= priležna kateta , a =
hipotenuza
|
|
|
a |
|
0 |
|
60 |
|
A |
|
B |
|
C |
|
a/2 |
|
a |
|
|
|
v |
|
a |
|
60 |
|
0 |
sin 60º =
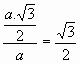
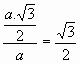
cos 60º =
tg 60º =
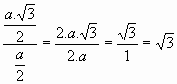
ctg 60º =
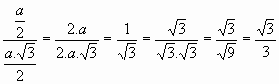
KOTNE FUNKCIJE KOTA 45º IZRA
ČUNAMO IZ ENAKOKRAKEGA PRAVOKOTNEGA TRIKOTNIKA, KI JE POLOVICA KVADRATA.Narisan je kvadrat , ki je z diagonalo razdjen na dva enakokraka trikotnika. Izrazi diagonalo s stranico a.
Slika:
|
B |
|
C |
|
D |
|
a |
|
d |
|
A |
|
a |
|
a |
|
a |
|
a |
|
a |
a = kateta
a = kateta
d = ? (hipotenuza)
Uporabi Pitagorov izrek:
d
= a
+
a
d
= 2a
d = a
diagonala kvadrata
3) za kot 45º
|
a |
|
d |
|
a |
|
A |
|
B |
|
C |
|
45 |
|
a |
|
d |
|
a |
|
0 |
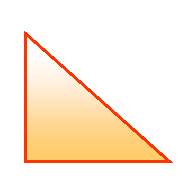
a = nasprotna kateta
a = priležna kateta
a.
= hipotenuza
sin 45º =
cos 45º =
tg 450 = 
ctg 450 =
P R I M E R I:
1)
Preveri s kalkulatorjem ali je sin 45º=
tako da najprej odtipkaš na kalkulatorju 45º in nato tipko sin, nato pa izrčunaš
še 
.Rezultata
morata biti enaka!
( Na kalkulatorju mora biti nastavitev deg).Tako lahko preveriš vrednosti za vse
kotne funkicije za kote 30º, 45º in
60º !
Izračunaj:
2) tg
60º. ctg 30º =3) 
=
4) 
=
KOTNE F
UNKCIJE KOTOV 0º IN 90º ODČITAJ S POMOČJO KALKULATORJATABELA:
|
a |
0º |
30º |
45º |
60º |
90º |
|
SIN |
0 |
|
|
|
1 |
|
COS |
1 |
|
|
|
0 |
|
TG |
0 |
|
1 |
|
¥ |
|
CTG |
¥ |
|
1 |
|
0 |
Z metodami, ki jih niti približno ne znaš razumeti, se dajo izračunati vrednosti kotnih funkcij za vsak kot poljubno natančno.
V teku stoletij so matematiki pripravili tabele za vsako stopinjo ali pa še bolj na gosto.V takih tablicah lahko najdeš vrednosti kotnih funkcij in jih od tam prepišeš.
Danes tudi tega ne boš delal. Uporabljal boš kalkulator, ki " zna " izračunati vrednosti kotnih funkcij za poljuben kot, samo na prave tipke je treba pritisniti.
Da boš lahko to počel pa moraš izraziti kot samo v stopinjah.
Pretvori v stopinje!
Pri vseh nalogah moraš upoštevati, da je
1' = 1/60º in da je 1'' = 1/3600ºa) 42º 45' = 42º + 45/60º = 42,75º
b) 42º 23' 18'' = ( 42º + 23/60º + 18/3600º) = 42,38833º
Nekateri kalkulatorji imajo za tak račun posebne tipke! ( ' ' ' , dms) !
Najdi jo na svojem kalkulatorju in jo uporabi
POZOR!
Kalkulatorji običajno znajo računati ali v stopinjah ali v radianih, le povedati jim je treba. V ta namen imajo pogosto posebno stikalo ali tipko, ki ga moraš pretakniti v položaj označen z
DEG za računanje s stopinjami in v položaj RAD za računanje z radiani.Za preverjanje ali imaš kalkulator prav nastavljen izračunaš za poskušnjo sin 90
º. Če je rezultat 1 računaš v stopinjah, če pa je rezultat 0,893996 pa je račun potekal v radianih.IZRAZI DANI KOT V STOPINJAH, MINUTAH IN SEKUNDAH
Tudi tukaj upoštevaš pretvornike:
1º = 60' in 1/10º ali 0,1º = 60º/10 = 6 min.1´ = 60'' in 1/10' ali 0,1' = 60/10 = 6 sek
1.primer
: 0.7º = 0,7 . 60' = 4,2 minute = 4' + 0,2 . 60'' = 1,2'' (zaokroži) = 1''Torej je 0,7º = 4' 1''
2.primer
: 32,4375º = 320 + 0.4375 . 60` (0,4375 . 60 = 26,25' = 26' + 0,25' ) in(0,25' = 0,25 . 60 = 15,0'')
Torej je: 32,4375º = 32º 26' 15''
Zamudno opravilo!
Tudi za ta postopek imajo nekateri kalkulatorji posebno tipko. Zapiši katero tipko moraš uporabiti na svojem kalkulatorju:…………………………………
Izračunaj zgornja primera in zapiši vrstni red tipk in številk za svoj kalkulator.
………………………………………………………………………………….
KAKO POIŠČEŠ VREDNOSTI KOTNIH FUNKCIJ ZA DANI KOT?
a) Poišči vrednost kotnih funkcij za kot
α = 24º 10' !Koraki:
1.Najprej kot 24º 10' pretvori v stopin
je24º 10'
= ( 24 + 10/60 )º = 24,1660(Pri nekaterih kalkulatorjih pretvarjanje ni potrebno)
2. Za računanje vrednosti kotne funkcije sin odtipkaj kot 24,1660 in tipko sin. sin 24,1660 = 0,4093816
( Pri nekaterih kalkulatorjih odtipkaš sin 240 10’ = )
Zapiši vrstni red tipk in številk za svoj kalkulator:
……………………………………………………………………………
3. Za računanje vrednosti kotne funkcije cos odtipkaj kot 24,1660 in tipko cos.
cos 24,1660 = 0,912363Zapiši vrstni red tipk in številk za svoj kalkulator:
……………………………………………………………………………
4. Za računanje vrednosti kotne funkcije tg odtipkaj kot 24,1660 in tipko tg.
tg 24,1660 = 0,448704
Zapiši vrstni red tipk in številk za svoj kalkulator:
……………………………………………………………………………
5. Za računanje kotne funkcije ctg pa nimš posebne tipke zato ravnaj takole.: ponovi postopek za računanje kotne funkcije tg 24,1660 nato pa pritisni tipko 1/x
tg 24,1660 = 0,448704 . 1/x = 2,228640 ctg 24,1660 = 2,228640
Zapiši vrstni red tipk in številk za svoj kalkulator:
……………………………………………………………………………
b) Poišči vrednost kotnih funkcij za kot 44
º 36' 50''!Koraki:
1.Najprej kot 44º 36' 50'' pretvori v stopinje:
44º 36' 50''= ( 44 + 36/60 + 50/3600 )º = 44,6188
02. Odtipkaj kot 44,61880 in tipko sin. sin 44,61880 = 0.7023256
Zapiši vrstni red tipk na svojem kalkulatorju:…………………………………..
3. Odtipkaj kot 44,61880 in tipko cos. cos 44,61880 = 0.711855
Zapiši vrstni red tipk na svojem kalkulatorju:…………………………………
4. Odtipkaj kot
44,61880 in tipko tg. tg 44,61880 = 0.9866121Zapiši vrstni red tipk na svojem kalkulatorju:………………………………….
5. Odtipkaj kot 44,61880 in tipko tg nato pa še tipko 1/x.
ctg 44,61880 = tg 44,61880
= 0.9866121 . 1/x = 1.013569ctg 44,61880 = 1.013569
Zapiši vrstni red tipk na svojem kalkulatorju:………………………………….
P R I M E R I!
1. Poišči vrednosti kotnih funkcij za kot 65
º 30' !sin 65º 30' =..............
cos 65º 30' =..............
tg 65º 30' =..............
ctg 65º 30' =......
........2. Poišči vrednosti kotnih funkcij za kot 24
º 10'sin 24º 10' =.................
cos 24º 10' =.................
tg. 24º 10' =.................
ctg. 24º 10' =..................
3. Poišči vrednosti kotnih funkcij za kot 68
º 34' 23''sin 68º 34' 23'' =......................
cos 68º 34' 23'' =......................
tg 68º 34' 23'' =........
..............ctg 68º 34' 23'' =......................
KAKO POIŠČEŠ KOT IZ NJEGOVE DANE VREDNOSTI KOTNE FUNKCIJE?
a) Iz vrednosti kotne fuknkcije sin a = 0,88835 izračunaj pripadajoči kot a v stopinjah, minutah in sekundah!Koraki:
Primer: shift sin 0,88835 = 62,666350
Zapiši vrstni red tipk na svojem kalkulatorju:………………………………….
2. Rezultat a = 62,666350 pretvori še v stopinje, minute in sekunde.
a = 620
Postopek poteka takole:
a = 62,666350
a = 620 . Decimalni del števila pomnoži s 60 in dobiš minute.
( 0,1stopinje = 60/10 stopinje = 6' ) 0,66635 x 60 = 39,981 minut.
Decimalni del ponovno pomnoži s 60 ( 0,1 minute = 60/10 sekunde = 6'' )
0,981 x 60 = 58,86 sekund = 59''( Decimalni del sekund zaokroži! )
a = 620 39' 59''
Zamudno! Raje se nauči s kalkulatorjem. Tudi za ta postopek ima kalkukator posebno tipko.
Shift dms 62.666350 = 620 39' 59''
Zapiši vrstni red tipk na svojem kalkulatorju:………………………………….
Če imaš dani kotni funkciji cos. in, tg pa uporabi tipke arccos, arctg ali cos-1 ali
tg-1 ali INV cos, INV tg. ( Funkcijo ctg pa moraš pretvoriti najprej v tg in nato uporabiti eno izmed tipk za pretvarjanje tg ; glej formulo v naslednjem poglavju!)
P R I M E R I :
sin x = 0,88835 x = …….0. ……’ ….….¨
cos x = 0,83549 x = …….0. ……’ ….….¨
tg x = 0,15243 x = …….0. ……’ ….….¨
ctg x = 0,23393 x = …….0. ……’ ….….¨
2. Poišči kot iz danih vrednosti kotnih funkcij!
sin µ = 0.83501 µ = …….0. ……’ ….….¨
cos µ = 0,99649 µ = …….0. ……’ ….….¨
tg µ = 0,15403 µ = …….0. ……’ ….….¨
ctg µ = 0,23148 µ = …….0. ……’ ….….¨
3. Poišči kot iz danih vrednosti kotnih funkcij!
sin x = 0,3456545 x = …….0. ……’ ….….¨
cos x = 0,2134543 x = …….0. ……’ ….….¨
tg x = 4,234355 x = …….0. ……’ ….….¨
ctg x = 2,345644 x = …….0. ……’ ….….¨
ZVEZE MED KOTNIMI FUNKCIJAMI ISTEGA KOTA
Koraki:
1.Načrtaj pravokotni trikotnik in označi kote in stranice!
2.Izrazi vrednosti kotnih funkcij za kot a z označenimi stranicami !
sin a =
cos a =
tg a =
ctg a =
Na osnovi Pitagorovega izreka lahko kotne funkcije med seboj povežeš in dokažeš sledeče povezave med njimi:
(sin a )2 piši sin2 a
sin2 a + cos2 a= 1
Dokaz:
sin2 a + cos2 a =
tg
a
= 
Dokaz:
= 
=
ctg
a
= 
Dokaz:
=
ctg
a
ZARADI TE ZVEZE FUNKCIJO KOTANGENS MANJKRAT UPORABI KER JE KALKULATORJI NE POZNAJO !
P R I M E R I:
1. Izračunaj vrednosti kotne funkcije cos a
, če je sin 
=
Uporabi obrazec, ki povezuje kotni funkciji sin α in cos α.
sin2
α + cos2 α = 1 Znane količine prenesi na desno stran enačbe.cos2
α = 1 - sin2 α Da dobiš cos α še koreni.cos2
α =
Vstavi vrednosti:
cos α =
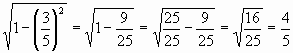
Izračunaj še vrednosti kotne funkcije tg in ctg !
Uporabi obrazec, ki povezuje tg, sin in cos kota
α.
Vstavi izračunane vrednosti!
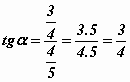
Uporabi še obrazec, ki povezuje funkciji tg in ctg!
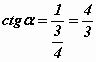
2. Izračunaj vrednosti kotne funkcije sin
α, če je cos α =
.
Uporabi obrazec, ki povezuje sin α in cos α.
sin2
α + cos2 α = 1 Znane količine prenesi na desno stran enačbe.sin2
α = 1 - cos2 α Da dobiš sin α še koreni.sin α =
Vstavi
vrednosti:
Nadaljuj sam!
Izračunaj sam še tg
α in ctg α ! (glej primer 1)RAZREŠEVANJE PRAVOKOTNEGA TRIKOTNIKA
Razrešiti pravokotni trikotnik se pravi, da iz dveh danih sestavin izračunaš vse druge trikotnikove sestavine
. Pri razreševanju pravokotnega trikotnika boš uporabil vse izreke ter definicije kornih funkcij.Pri razreševanju pravokotnega trikotnika je možnih pet osnovnih primerov.Pri vsakem moraš obvezno narediti skico:
P R I M E R I:
1
. Dani sta kateti a in b; izračunaj hipotenuzo c ter oba ostra kota α in b(a = 21cm, b = 28cm, c = ?
α = ? b = ?)|
C |
|
A |
|
B |
|
a |
|
b |
|
c |
Kot α dobi
š iz definicije tgα.tg α = a/b
tg α = 21/
28 = 0,75tg α = 0,75
α
= 360 52' 12''Kot b
je kotu α komplementaren. α + b = 900b = 900
- αb = 900 – 360 52' 12''
b = 530 7' 48''
Hipotenuzo c dobiš iz Pitagorovega izreka:
c2 = a2 + b2
c2 = 212 + 282 = 441 + 784 =
= 35
c = 35cm
Hipotenuzo c pa lahko izračunaš še takole:
a = c . sinα; c = a/sinα = 21/sin 36
0 52' 12'' = 21/0,60000 = 35c = 35cm
2. Dani sta ena kateta, npr. kateta b in hipotenuza c; iščemo drugo kateto a ter oba ostra kota
α in b . ( b = 31,54cm,c = 48,69cm, a = ? α =? b = ?)
Kot b dobiš iz definicije za sin b . Skica:
|
C |
|
A |
|
B |
|
a |
|
b |
|
c |
sinb = b/c
sinb = 31,54/48,69 = 0,64777
b = 400 22' 25''
Kota α in b
sta komplementarna, torej je:α + b
= 900α = 90
0 - bα = 90
0 – 400 22' 25''α
= 490 37' 35''Kateto a lahko izračunaš po Pitagorovem izreku
a2 = c2 – b2
ali pa:
a = c . sin α = 48,69 . sin 49 37' 35'' = 48,69. 0,761836733 = 37,09
a = 37,09cm
3. Dana je hipotenuza c in eden od ostrih kotov npr.kot b ; poišči kateti a in b ter kot b
( c = 8,5cm, b = 240 35', a = ? b =? b =?)
Kot α je: Skica:
|
C |
|
A |
|
B |
|
a |
|
b |
|
c |
α + b = 900
α = 90
0 – 240 35'α
= 650 25'Iz definicij za kotne funkcije dobiš:
sin α = a/c
a = c . sin α = 8,5 . 0,912120 =
7,753a = 7,8 cm
cos α = b/c
b = c . cos α = 8,5 . 0,4160162 = 3,536 = 3,5
b = 3,5 cm
4. Dana je ena kateta npr.kateta a in njej nasprotni kot
α; poišči drugo kateto b, hipotenuzo c ter kot b , ( a = 14,2m, α = 680 12', b = ? c = ? b = ?)α + b
= 900 Skica:|
A |
|
B |
|
C |
|
a |
|
b |
|
c |
b = 900
- αb = 900 – 680 12'
b
= 210 48'Iz definicije kotne funkcije ctg b izračunaj še b.
ctg b = a/b
b = a . ctg b = 14,2 . 0,39998 = 5,6795
b = 5,68cm
Hipotenuzo c izračunaj npr. iz:
sinα =
a/ca = c . sin α
c = a/sin α = 14,2/0,92849 = 15,293
c = 15,29cm
5. Dana je ena kateta npr. kateta b in njej priležni kot
α; poišči drugo kateto a, hipotenuzo c ter kot b ( b = 11cm, α = 500 30', a = ? c = ? b = ? )α + b
= 900b = 900
- α|
A |
|
B |
|
C |
|
a |
|
b |
|
c |
b = 900 – 500 30'
b
= 390 30'Iz definicij dobiš:
tg α = a/b
a = b . tg α = 11.1,2131 = 13,3441
a = 13,3cm
sin b = b/c
b = c . sin b
c = b/sin b = 11/0,63608 = 17,292
c = 17,3cm
ŠE NEKAJ PRIMEROV ZA RAZREŠEVANJE PRAVOKOTNEGA TRIKOTNIKA IN UPORABO V PRAKSI !
1. Stopnice se dvigajo v kotu 250. Izračunaj višino ene stopnice, če je širina ene stopnice 26cm!
V pravokotnem trikotniku,
|
v |
|
š |
|
š |
|
v |
ki ga tvorijo višina stopnice v,
širina stopnice š ter smer dviganja – kot j ,
izračunaj danemu kotu j nasprotno kateto.
tg j = v/š
v = š . tg j
v = 26 . tg 250
v = 26.0,46631
v = 12,124
v = 12,1cm Stopnica je visoka 12,1cm.
2. 2,5m dolg navpično postavljen drog meče na vodoravna tla 3m dolgo senco. Izračunaj naklonski kot svetlobnih žarkov proti vodoravni ravnini!
d – drog = 2,5m
|
s
|
|
d
|
s – senca = 3m
tg w = d/s
tg w = 2,5/3 = 0,8333333
w = 390 48' 20''
Naklonski kot žarkov je 390 48' 20''.
3. Vzpon ceste je 5,5%; za koliko je ta cesta nagnjena proti vodoravni ravnini? Izračunaj tudi višinsko razliko dveh krajev ob tej cesti, ki sta oddaljena drug od drugega 2km!
Vzpon ceste je razmerje med višinsko razliko dveh točk na tej cesti in med vodoravno razdaljo teh dveh točk. Vzpon 5,5 % ali 5,5/100 pomeni,da se cesta na vsakih 100m vodoravne razdalje dvigne za 5,5m.
tg d = 5,5/100
|
100m |
|
5,5m |
tg d = 0,055
d = 30 8' 53''
Cesta je proti vodoravni ravnini nagnjena za 30 8' 53''.
Kraja, ki imata vodoravno razdaljo d = 2km imata višinsko razliko v.
tg d = v/d
|
d |
|
v |
v = d . tg 30 9'
v = 2000.0,055
v = 110m
Višinska razlika teh dveh krajev je 110m.
4. Kolikšna je vlečna sila motorja, ki vleče 1500kg težak avto po tračnicah na vlečno vozilo pod kotom 320 (trenja ne upoštevaj).
Avto, ki tehta 1500kg ima težo 15000N; premagovati je treba le dinamično komponento teže,ki jo označi z Fd; dobiš jo tako,da težo F razstaviš s paralelogramom sil v dve komponenti, ki sta druga na drugi pravokotni. To sta dinamična komponenta Fd in statična komponenta Fs.
Silo Fd izračunaj iz pravokotnega trikotnika, v katerem poznaš hipotenuzo F ter kot j .
sin j = Fd/F
|
Fd |
|
j |
|
j |
|
F |
Fd = F . sin j
Fd = 1500 . sin 320
Fd = 15000 . 0,52992
Fd = 7948,8N
Vlečna sila motorja je 7948,8N.
5. Daljica a = 27cm je proti projekcijski ravnini naklonjena za kot e = 530 18'. Izračunaj dolžino njene pravokotne projekcije na to ravnino!
Na sliki je daljica A'B', ki je pravokotna projekcija daljice AB = a na ravnino P . Iz pravokotnega trikotnika DBA, ki ga dobiš, če daljico A'B' vzporedno premakneš do točke D izračunaš njeno dolžino a'. ( DB = A'B' = a' )
cos e = a'/a
|
A |
|
B |
|
D |
|
A` |
|
B` |
|
a |
|
a` |
a' = a . cos e
a' = 27 . cos 530 18'
a' = 27 . 0,59763
a' = 16,136
a' = 16,136cm
Pravokotna projekcija te daljice meri 16,14cm.
6. S 45m visoke stolpnice opazuješ drevo. Kako daleč je to drevo od podnožja stolpnice, če ga vidiš pod kotom 20 30' ?
B
C A
Vrh stolpnice B, njeno podnožje C in drevo A tvorijo pravokotni trikotnik v katerem poznamo kateto v ter kot 20 30'.
ctg 20 30' = d/v
d = v . ctg 20 30'
d = 45 . ctg 20 30' (ctg 20 30' = 1/tg 20 30')
d = 45. 22,90377
d = 1030,669
d = 1030,7m
Drevo je oddaljeno od vznožja stolpnice 1030,7m.
RAZREŠEVANJE ENAKOKRAKEGA TRIKOTNIKA
Enakokraki trikotnik
razdeli z višino v, ki jo načrtaš na osnovnico c, na dva skladna pravokotna trikotnika..Če dodaš k sestavinam nastalega pravokotnega trikotnika še višino v, lahko izračunaš iz katerihkoli dveh neodvisnih sestavin vse druge, to je razrešiš enakokraki trikotnik.
Z enakokrakim trikotnikom si pomagaš
|
A |
|
B |
|
C |
|
a |
|
a |
|
c |
|
c/2 |
|
v |
|
v |
|
a |
tudi pri drugih likih. O tem kasneje ! a2 = v2
+ 
P R I M E R I:
1. Reši enakokraki trikotnik s podatkoma a = 12cm, a = 670 35'.
( b = ? , c = ? , v = ? )
Iz 2 . a + g = 1800 dobiš:
g = 180 – 2 . 670 35'
g = 1800 – 1350 10'
g = 440 50'
|
A |
|
B |
|
C |
|
c |
|
v |
|
a |
|
a |
|
a |
|
v |
|
c/2 |
cos a = (c/2)/a
c = 2a . cos a
c = 24 . cos 670 35'
c = 24 . 0,38133 = 9,15192
c = 9,15cm
sin a = v /a
v = a . sin a
v = 12 . sin 670 35'
v = 12 . 0,92444
v = 11,09328
v = 11,1cm
2. Reši enakokraki trikotnik s podatkoma c = 10cm, g = 320 18'!
( a = ?, a = ?, v = ? )
|
A |
|
B |
|
C |
|
a |
|
a |
|
c |
|
c/2 |
|
v |
|
v |
|
a |
sin 
=
a .sin =
a = 
= 
=
a = 17,975cm
cos =
Iz 2 . a
+ g = 1800 dobiš:
a . cos = v 2.a
= 1800 - g
15,87. 0,960536 = v a = (1800 - g )/2
a = (1800 – 320 18`)/2
v = 15,24cm a
= 730 51´3. Reši enakokraki trikotnik s podatki v = 6,5cm, a = 180 44' !
( a = ? c = ? g = ? )
|
A |
|
B |
|
C |
|
a |
|
a |
|
c |
|
c/2 |
|
v |
|
v |
|
a |
sin a =
a . sin a = v
a = 
=
= 
a = 20,24cm
cos a = 
a . cos a =
Iz 2 . a
+ g = 1800 dobiš:
2 .a . cos a = c g = 180 – 2 . 180 44'
2 . 20,24 .cos 180 44’ = c g = 1800 – 370 28'
2 . 20,24 . 0,9470235 = c g = 1420 32'
c = 38,34cm
RAZREŠEVANJE RAZNOSTRANIČNEGA TRIKOTNIKA
Definicije kotnih funkcij in Pitagorov izrek nam omogočajo, da znaš razrešiti vsak pravokotni trikotnik!
Tudi raznostranični trikotnik je možno razrešiti z uporabo kotnih funkcij, to se pravi izračunati vse njegove osnovne sestavine ( stranice in kote).
Za razreševanje raznostraničnega trikotnika moraš poznati dva izreka in sicer
sinusni izrek in cosinusni izrek.GLEJ SINUSNI IZREK !
P R I M E R I:
a) znana je ena stranica in dva kota!
1. Reši trikotnik s podatki c = 8cm, a = 340 18' , b = 620 39'
Izračunati moraš ostale osnovne trikotnikove sestavine, to sta še dve stranici a in b in trtetji kot g .
Iz a + b + g =1800 sledi: Skica:
|
A |
|
B |
|
C |
|
c |
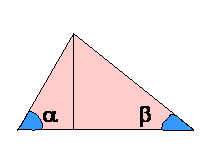
g = 1800- (a + b )
g = 1800 - (340 18' + 620 57')
g = 1800 – 960 57'
g = 830 3'
Upoštevaj, da je produkt zunanjih členov sorazmerja enak produktu notranjih členov
Iz a : c = sin a : sin g in b : c = sin b : sin g dobiš:
a . sin g = c . sin a (Deli s sin g !) in b . sin g = c . sin (Deli s sin g !)
a = c . sin a /sin g b = c . sin b / sin g
Vstavi dane podatke in opravi računske operacije:
a = 8 . sin 340 18' / sin 830 3' b = 8 . sin 620 39' / sin 830 3'
a = 8 . 0,56353 / 0,99266 b = 8 . 0,88822 / 0,99266
a = 4,54 = 4,5cm b = 7,15 = 7,2
a = 4,5cm
b = 7,2cmSedaj poznaš vse trikotnikove osnovne sestavine; vse stranice in vse kote.
b) Znani sta dve stranici in kot, ki leži eni od njih nasproti.
1. Reši trikotnik s podatki a = 10cm, b = 8cm, a
= 48º 13'Skica:
|
A |
|
B |
|
C |
|
a |
|
b |
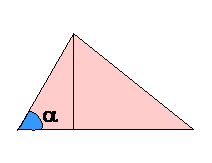
a : b= sin a : sin b
a . sin b = b . sin a /a
sin b = b . sin a /a
sin b = 8 . sin 48º13' / 10 = 8 . 0,74567/10 = 0,59654
sin b = 0,59654
b
= 36º37'Kot g dobiš iz obrazca: a + b + g
= 180ºg
= 180º - (a + b )g
= 180º- ( 48º13' + 36º37')= 180º - 84º50' = 95º10'g =
95º10'Tudi stranico c izračunaš po sinusnem izreku:
c : a = sin g : sin a
c = 
c =
c = 13,4cm
GLEJ KOSINUSNI IZREK!
P R I M E R I:
a) Znani sta dve stranici in kot, ki ga oklepata:
1. Reši trikotnik s podatki a = 7m, b = 5,5m, g
= 54º31'c = ? a = ? , b = ? Skica:
|
A |
|
B |
|
C |
|
a |
|
b |
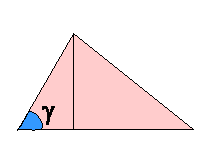
Uporabi kosinusni izrek :
c2 = a2 + b2 – 2.a.b.cos g
c2 = 72 + 5,52
- 2.7.5,5.cos 54º31'c2 = 49+30,25 - 77.0,58046
c2 = 34,5548
c =
=5,878 =5,88
c = 5,88m
Kot a bi lahko izračunal po sinusnem izreku sin a : sin g = a : c !
Izračunal ga boš iz kosinusnega izreka:
a2 = b2 + c2 – 2.b.c.cos a
a2 - b2 - c2 = - 2bc.cos a /(-1)
b2 + c2 - a2 = 2bc.cos a / delimo z 2bc
cos a =
cos a =
cos a = 0,24466
a
= 75º50'Kot b dobiš iz obrazca za vsoto kotov v triktniku.
b = 1800 – ( a + g )
b = 1800
– ( 75º50' + 54º31' )b = 1800 – 1300 21'
b = 490 38'
b) Znane so vse tri stranice trikotnika:
1. Reši trikotnik s podatki a = 95cm, b = 102cm, c = 120cm
a , b , g = ?
Iz a2 = b2 + c2 – 2. b . c .
cos a dobiš cos a =
|
A |
|
B |
|
C |
|
a |
|
b |
|
c |
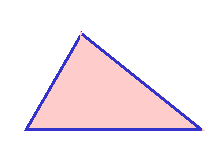
Iz b2 = a2 + c2 – 2. a . c .
cos b dobiš cos b =
iz c2 =a2 + b2 – 2. a. b . cos
g dobiš cos g =
cos
a = 49052’
Izračunaj še ostala kota.
cos b = ……………. cos g =…………….
b = ………………… g = ……………….
POLMER TRIKOTNIKU OČRTANEGA KROGA
Načrtaj raznostranični trikotnik ABC ter mu očrtaj krog! Središče trikotniku očrtanega kroga S dobiš tako, da načrtaš simetrale stranic.
sa - simetrala stranice a
|
A |
|
B |
|
C |
|
s |
|
s |
|
s |
|
a |
|
b |
|
c |
|
a |
|
b |
|
c |
|
S |
|
R |
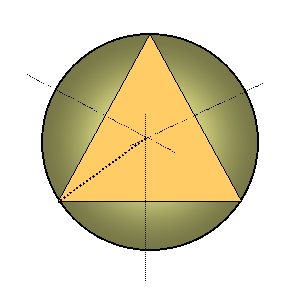
sb- simetrala stranice b
sc- simetrala stranice c
S – središče trikotniku oćrtanega kroga
R – polmer trikotniku očrtanega kroga
Poglej poglavje o sinusnem izreku in zapiši formule, kjer nastopa polmer trikotniku očrtanega kroga.
Ti obrazci so: a = 2 . R . sina , b = 2 . R . sinb , c = 2 . R . sing
Zapiši še formule za ploščino trikotnika, če je znan kot in ustrezni stranici.
,
, 
Iz obrazca in
obrazca a = 2 . R . sin a izrazi sin
a .
in
Obrazca izenači:
Iz obrazca izpelji količino R.
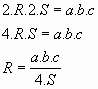
Uporabi še kakšen drug par ustreznih obrazcev in se prepričaj o pravilnosti obrazca!
POLMER TRIKOTNIKU VČRTANEGA KROGA
Načrtaj raznostranični trikotnik ABC ter mu krog včrtaj!
Središče trikotniku včrtanega kroga dobiš tako, da načrtaš simetrale kotov.
sa - simetrala kota a
|
A |
|
B |
|
C |
|
s |
|
s |
|
s |
|
S |
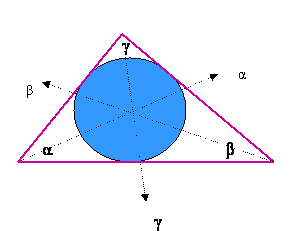
sb - simetrala kota b
sg - simetrala kota g
S- središče trikotniku včrtanega kroga
Simetrala kota, kot razpolavlja. Vsaka točka na imetrali kota je od obeh krakov enako oddaljena.
Načrtaj še enkrat poljuben raznostranični trikotnik in mu včrtaj krog!
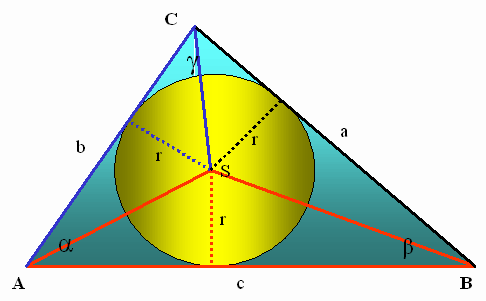
Središče trikotniku včrtanega kroga poveži z vsemi oglišči. S tem si razdelil trikotnik ABC v tri trikotnike ABS, BCS, in CAS, ki imajo osnovnice c, a in b. Višina vsakega od njih je enaka polmeru včrtanega kroga, ki ga iščeš.
r - polmer trikotniku včrtanega kroga.
Ploščina trikotnika ABC je enaka vsoti ploščin vseh treh prej omenjenih trikotnikov.
S ABC= S ABS + S BCS + S CAS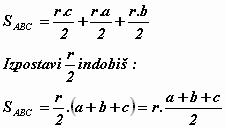
Dogovor je, da označiš izraz (a + b + c)/2, ki je enak polovici obsega trikotnika s črko s.
Torej je :
Iz enačbe S = r . s izraziš r
r = S / s
Torej je:
s = (a + b + c)/2 S = s . r r = S / s
r - polmer trikotniku včrtanega kroga
Izpelji še obrazce za polmer očrtanega in včrtanega kroga za enakostranični trikotnik
1. Polmer včrtanega kroga
s = ( a + a +a)/2 = 3a/2
S =
polmer enakostraničnemu
trikotniku včrtanega kroga
2. Polmer očrtanega kroga
polmer enakostraničnemu trikotniku očrtanega kroga