SPLOSNI POJMI
Home Up SPLOSNI POJMI POVSINA PRIZME PROSTORNINA PRIZME PRIMERI- PRIZMA NALOGE - PRIZMA

 

 

PRIZMA

  Ob obsegu poljubnega mnogokotnika drsi premica, ki ne leži v njegovi ravnini., in sicer tako, da ostane ves čas vzporedna svoji prvotni legi.. Premica opiše lomljeno ravno ploskev, ki jo sestavlja toliko sekajočih se ravnin, kolikor stranic ima mnogokotnik, navzgor in navzdol pa ni omejena. Ta ploskev omejuje del prostora, ki se imenuje prizmatični prostor.

 

Če prizmatični prostor presekaš z dvema vzporednima ravninama, dobiš od vseh strani omejen del prostora, to je geometrijsko telo, ki se imenuje prizma.

 

 

 

 

 

 

 

 

                   Prizmatični prostor                                                      Prizma

 

A

B

C

D

E

A

A

B

B

C

C

D

D

A

A

A

B

B

B

C

C

C

D

E

d

S

S

S

S

S

S
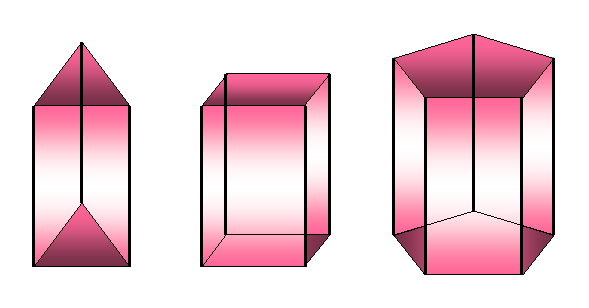Telesa na slikah so prizme. Na njih vidiš, da omejujeta vsako prizmo dva skladna in vzporedna mnogokotnika, ki se imenujeta osnovni ploskvi in toliko paralelogramov, koliko ima osnovna ploskev stranic. Ti paralelogrami so stranske ploskve prizme in tvorijo njen plašč. Če plašč in osnovni ploskvi razgrneš v ravnino, dobiš mrežo prizme.

 

 

 

 

 

 

 

 

 

 

A

B

C

D

E

A

A

B

B

C

C

D

D

A

A

A

B

B

B

C

C

C

D

E

a

b

c

d

e

a

a

b

b

b

c

c

c

b

b

c

c

d

d

d

e

e
Stranice obeh osnovnih ploskev so osnovni robovi prizme. V vsakem osnovnem robu se stikata po ena osnovna in ena stranska ploskev. Po dve stranski ploskvi se stikata v stranskem robu. Vsi stranski robovi so med seboj vzporedni in enako dolgi.

 

 

 

 

 

 

 

 

  

A

B

C

D

E

A

A

B

B

C

C

D

D

A

A

A

B

B

B

C

C

C

D

E

d

s

s

s

s

s

s

s

s

s

s

s

s
a, b, c, d, e…osnovni robovi

 

 

 

 

 

 

 

 s – stranski robovi

 

A

B

C

D

E

A

A

B

B

C

C

D

D

A

A

A

B

B

B

C

C

C

D

E

d

Stranske ploskve

Stranske ploskve

Stranske ploskve
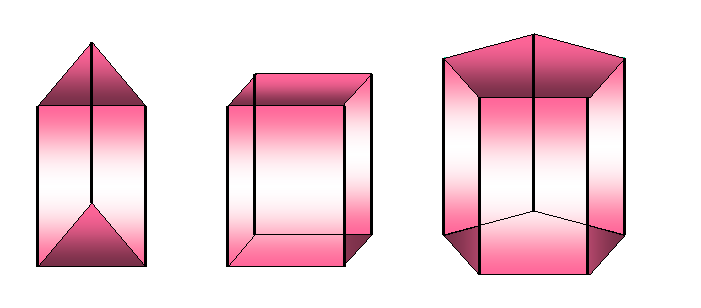Po številu stranskih robov ali po številu osnovnih robov ene osnovne ploskve razlikuješ  tristrane, štiristrane,…n - strane prizme.

 

 

 

 

 

 

 

 

 

A

B

C

D

E

A

A

B

B

C

C

D

D

A

A

A

B

B

B

C

C

C

D

E

v

v

v
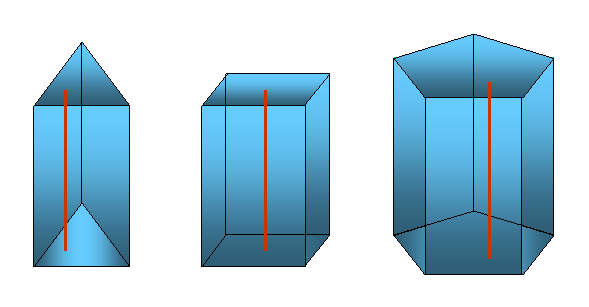Če so stranski robovi pravokotni na osnovno ploskev, je prizma pokončna, njene stranske ploskve so pravokotni paralelogrami ( kvadrat in pravokotnik). Prizme na slikah so pokončne.. Pravokotna razdalja obeh osnovnih ploskev je višina prizme.Višina pokončne prizme je enaka stranskemu robu.

 

 

 

 

 

 

 

 

 v – višina prizme

  Če stranski robovi niso pravokotni na osnovnih ploskvah, je prizma poševna. Njene stranske ploskve so poševnokotni paralelogrami (rombi in romboidi). Prizmi na slikah sta poševni.

 

 

 

 

 

 

 

 

                        Poševna tristrana   prizma                              Poševna štiristrana  prizma

 

Pokončna prizma, ki ima za osnovno ploskev pravilen mnogokotnik (enakostraničen trikotnik, kvadrat, pravilni 5, 6, 7...- kotnik itd.), je pravilna.

 

A

B

C

D

E

A

A

B

B

C

C

D

D

A

A

A

B

B

B

C

C

C

D

E

a

a

a

a

a

a

a

a

a

a

a

a

Pravilna

Pravilna

Pravilna

tristrana

štiristrana

šeststrana

prizma

prizma

prizma
 

 

 

 

 

 

 

 

 

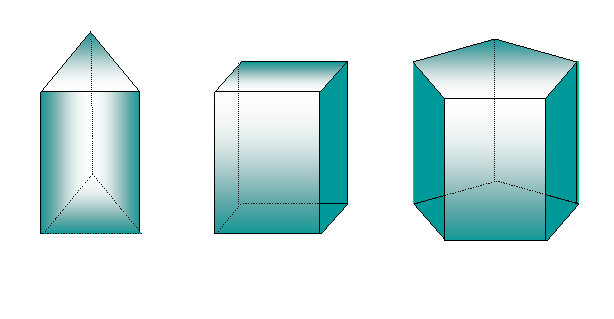
Prizma, ki ima vse robove enako dolge, je enakorobna. Stranske ploskve pravilne prizme so skladni pravokotniki, stranske ploskve pravilne enakorobne prizme pa so kvadrati.

A

B

C

D

E

A

A

B

B

C

C

D

D

A

A

A

B

B

B

C

C

C

D

E

a

a

a

a

a

a

a

a

a

a

a

a

Enakorobna

Enakorobna

Enakorobna

tristrana

štiristrana

šeststrana

prizma

prizma

prizma
 

 

 

 

 

 

 

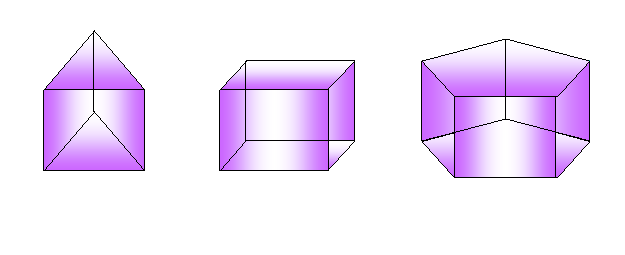
 Prizma, ki ima za osnovno ploskev paralelogram, se imenuje tudi paralelepiped.

 Omejujejo ga sami paralelogrami. Pokončni paralelepiped, ki ima za osnovno ploskev pravokotnik, se imenuje kvader. Enakorobni kvader je kocka.

 

a
Text Box: a

a
Text Box: a

a
Text Box: a Text Box: Kocka Text Box: Kvader

a
Text Box: a

c
Text Box: c

b
Text Box: b

 

 

 

 

 

 

 Če presekaš prizmo z ravnino, ki je vzporedna osnovnima ploskvama, dobiš vzporedni presek, ki je z osnovno ploskvijo skladen mnogokotnik.

A

A

B

B

C

C

D

A

A

B

B

C

D

C

Vzporedni presek

 

 

 

 

 

 

 

 

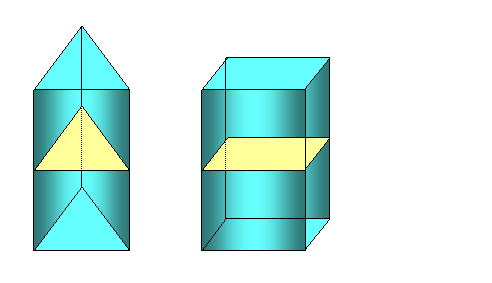
 Če presekaš prizmo skozi dva njena nesosedna stranska roba, dobiš diagonalni presek.

Ta presek gre skozi enakoležni diagonali osnovnih ploskev in je pri pokončni prizmi pravokotnik.

D

D - telesna diagonala

b

c

a

d

a

d

c

D

d

b

b

c

a

d

D

d

d

d

Pr

Pr

Pr

Pr - diagonalni preseki

 

 

 

 

 

 

 

 

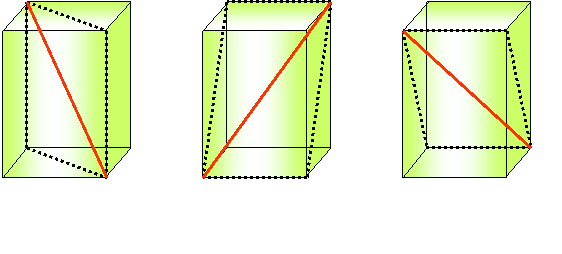
 Diagonale diagonalnih presekov so telesne diagonale prizme. Ne smeš jih zamenjati z diagonalo katerekoli od mejnih ploskev prizme.