Večkotniki (splošno)

Večkotnik je ravninski lik, ki ga omejuje enostavno sklenjena lomljena črta.
Enostavno sklenjena lomljena črta (lomljenka) je črta sestavljena iz daljic, od katerih se zaporedni dve stikata v skupnem krajišču, zadnja daljica se stika s prvo. Drugih presečišč te daljice nimajo, prav tako se v nobeni točki ne stikata več kot dve daljici. Dve zaporedni daljici praviloma ne smeta ležati na skupni premici.
Te daljice imenujemo stranice večkotnika, krajišča teh daljic pa so oglišča večkotnika. Oglišči, ki ju povezuje stranica, sta sosednji oglišči.

Notranji kot v večkotniku je kot, ki ima vrh v oglišču, kraka pa ležita na stranicah. (Notranjost kota mora imeti z notranjostjo večkotnika neprazen presek.)

Zunanji kot večkotnika je sokot notranjega kota. Zunanji kot obstaja, če je notranji kot manjši od 180°.

Večkotnik, ki ima točno n oglišč, ima tudi točno n stranic. Imenujemo ga n-kotnik.

Pravilni n-kotnik je n-kotnik, ki ima vse stranice skladne in vse notranje kote skladne.

Konveksni večkotnik lahko dobimo kot presek polravnin, ki jih določajo nosilke stranic.
Pravilni n-kotnik je vedno konveksen.

Večkotniki

Vsota kotov v n-kotniku

Vsota notranjih kotov v poljubnem konveksnem n-kotniku je enaka:
S_n = (n − 2) 180°

Vsota zunanjih kotov v poljubnem konveksnem n-kotniku je enaka:
S_n' = 360°

Diagonale v n-kotniku

Diagonala večkotnika je daljica, ki povezuje dve nesosednji oglišči.

Število diagonal n-kotnika lahko izračunamo po formuli:

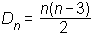
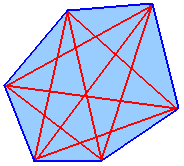
Zgled: Šestkotnik ima devet diagonal.
Diagonale

Kazalo poglavij

Simetrija - simetrale

Trikotniki

Abecedno kazalo