Trikotniki

Standardno označevanje trikotnika:
Oglišča označimo s črkami A, B, C.
Stranico, ki leži nasproti oglišču A (oziroma B, C) označimo a (oziroma b, c).
Notranji kot pri oglišču A (oziroma B, C) označimo α (oziroma β, γ), ustrezni zunanji kot pa α' (oziroma β', γ').

Lastnosti trikotnika

Vsota notranjih kotov v poljubnem trikotniku je 180°, vsota zunanjih kotov pa je 360°, torej:
  α + β + γ = 180°
  α' + β' + γ' = 360°

Zunanji kot v trikotniku je enak vsoti notranjih nepriležnih kotov:
  α' = β + γ
  β' = α + γ
  γ' = α + β

V trikotniku leži nasproti večji stranici vedno večji kot in obratno:
  a > b ⇔ α > β

Za stranice trikotnika velja trikotniška neenakost: dolžina poljubne stranice je vedno manjša kot vsota ostalih dveh stranic, torej:
  a < b + c
  b < a + c
  c < a + b

Računanje stranic in kotov imenujemo razreševanje trikotnika. V poljubnem trikotniku si pri tem pomagamo z naslednjima izrekoma:

Kosinusni izrek:
  a² = b² + c² − 2bc cos α
  b² = a² + c² − 2ac cos β
  c² = a² + b² − 2ab cos γ
Sinusni izrek:

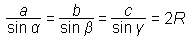
(število R pomeni radij očrtane krožnice, glej spodaj)

Glej tudi poglavje: Obseg in ploščina

Vrste trikotnikov

Glede na stranice delimo trikotnike na tri skupine:

Enakostranični trikotnik ima vse tri stranice enako dolge. Posledica: tudi vsi trije notranji koti so skladni.
Pravimo mu tudi pravilni trikotnik.
Enakokraki trikotnik ima točno dve stranici enako dolgi. Ti dve stranici imenujemo kraka, tretjo stranico imenujemo osnovnica. Kota ob osnovnici sta skladna.
Raznostranični trikotnik ima vse tri stranice različno dolge. Posledica: tudi koti v raznostraničnem trikotniku so različno veliki.

Glede na notranje kote delimo trikotnike na tri skupine:

Ostrokotni trikotnik ima tri ostre (notranje) kote.
Pravokotni trikotnik ima en pravi kot (ostala dva notranja kota pa sta ostra).
Glej poglavje: pravokotni trikotnik.
Topokotni trikotnik ima en topi notranji kot (ostala dva kota pa sta ostra).

Principi skladnosti trikotnikov

Skladnost trikotnikov lahko preverjamo z naslednjimi štirimi principi:

Princip SSS:
Če se trikotnika ujemata v dolžinah vseh treh stranic, potem sta skladna.
Princip SKS:
Če se trikotnika ujemata v dolžinah dveh stranic in v kotu med njima, potem sta skladna.
Princip KSK:
Če se trikotnika ujemata v dolžini ene stranice in v dveh kotih, potem sta skladna.
Princip SsK:
Če se trikotnika ujemata v dolžinah dveh stranic in v kotu, ki leži nasproti večji od njiju, potem sta skladna.

Značilne točke trikotnika

Težišče

Težiščnica trikotnika je daljica, ki povezuje oglišče in razpolovišče nasprotne stranice.
Vse tri težiščnice se sekajo v eni točki. To točko imenujemo težišče trikotnika (ali baricenter).
Težišče deli vsako od težiščnic v razmerju 1 : 2.

Višinska točka

Višina trikotnika je daljica, ki poteka od oglišča do nosilke nasprotne stranice in je nanjo pravokotna.
Nosilke vseh treh višin se sekajo v eni točki. To točko imenujemo višinska točka (ali ortocenter).
Klikni tukaj za gibljivi prikaz.

Središče očrtane krožnice

Simetrale vseh treh stranic trikotnika se sekajo v eni točki. Ta točka je središče očrtane krožnice. Očrtana krožnica poteka skozi vsa tri oglišča trikotnika. Vse tri stranice trikotnika so tetive te krožnice.
Klikni tukaj za gibljivi prikaz.

Središče včrtane krožnice

Simetrale notranjih kotov trikotnika se sekajo v eni točki. Ta točka je središče včrtane krožnice. Včrtana krožnica ima vse tri stranice trikotnika za tangente.
Klikni tukaj za gibljivi prikaz.