Podobnost

Podobni trikotniki

Trikotnika ΔABC in ΔA'B'C' sta podobna, če se ujemata v vseh treh kotih: α = α', β = β', γ = γ'.
Podobnost označimo z znakom ~, torej: ΔABC ~ ΔA'B'C'.

Podobna trikotnika imata stranice v enakem razmerju, torej:
  a' : a = b' : b = c' : c    oziroma    a' : b' : c' = a : b : c

Vrednost razmerja med istoležnima stranicama imenujemo koeficient podobnosti k:
  a' : a = k,   b' : b = k,   c' : c = k
oziroma:
  a' = ak,   b' = bk,   c' = ck.

Središčni razteg

Središčni razteg s središčem S in s koeficientom k (k ≠ 0) je preslikava, ki preslika poljubno točko T v točko T' tako, da velja:
- točke S, T in T' ležijo na isti premici p
- če je k > 0, potem ležita T in T' na istem poltraku s krajiščem v S;
če je k < 0, pa leži S med T in T'
- |ST' | = |k| |ST|

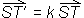
Središčni razteg lahko opišemo tudi kot množenje vektorja s skalarjem: Vektorsko

Središčni razteg se imenuje tudi dilatacija ali homotetija.
Če s središčnim raztegom preslikamo premico p, dobimo kot rezultat premico p', ki je prvotni premici vzporedna.

Če preslikamo poljuben lik s središčnim raztegom, se pri tem koti ohranijo (ostanejo enako veliki), dolžine stranic (in tudi diagonal, višin, ipd.) pa se pomnožijo s |k|. (Ploščina lika se pomnoži s k².)

Če preslikamo s središčnim raztegom poljuben trikotnik, je dobljeni trikotnik prvotnemu podoben. Zato se odločimo, da bomo definirali podobnost za ostale like s pomočjo središčnega raztega:

Podobnost (splošno)

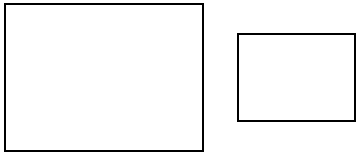
Množici točk M₁ in M₂ sta med seboj podobni, če lahko eno preslikamo na drugo s preslikavo, ki je sestavljena iz togega premika in središčnega raztega.

Zgled: Naslednja pravokotnika sta podobna:
Podobna štirikotnika

Opozorilo:
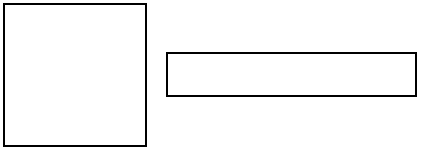
Ujemanje v kotih na splošno ne zadostuje za podobnost.
Zgled: Spodnja štirikotnika nista podobna, čeprav se ujemata v vseh štirih kotih.
Štirikotnika nista podobna