| Kazalo poglavij | Pravokotni trikotnik | Podobnost | Abecedno kazalo |
Štirikotniki
Paralelogram
Štirikotnik, ki ima dva para vzporednih stranic, imenujemo paralelogram.
Lastnosti paralelograma:
Nasprotna kota v paralelogramu sta skladna (α = γ, β = δ).
Kota v sosednjih ogliščih sta suplementarna (α + β = 180°, β + γ = 180°, γ + δ = 180°, δ + α = 180°).
Stranici, ki sta vzporedni, sta tudi enako dolgi, torej: a = c, b = d.
Ta lastnost je za paralelogram karakteristična: Če za neki štirikotnik velja a = c in b = d, potem je ta štirikotnik zagotovo paralelogram.
(Velja tudi: Če sta v nekem štirikotniku dve stranici vzporedni in enako dolgi, potem je ta štirikotnik zagotovo paralelogram.)
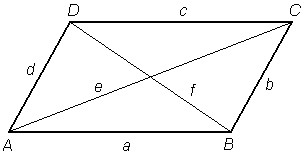
Diagonali paralelograma se med sabo razpolavljata.
Tudi ta lastnost je karakteristična: Če se v nekem štirikotniku diagonali med sabo razpolavljata, potem je ta štirikotnik zagotovo paralelogram.
Vrste paralelogramov:
Paralelogram, ki ima vse štiri stranice skladne, imenujemo romb.
Diagonali romba razpolavljata notranje kote romba.
Diagonali romba sta med sabo pravokotni. (Ta lastnost je v nekem smislu karakteristična: Če sta v nekem paralelogramu diagonali pravokotni, potem je to gotovo romb.)
Rombu lahko vedno včrtamo krožnico. Stranice romba so tangente te krožnice, zato pravimo, da je romb tangentni štirikotnik.
Diagonali romba razpolavljata notranje kote romba.
Diagonali romba sta med sabo pravokotni. (Ta lastnost je v nekem smislu karakteristična: Če sta v nekem paralelogramu diagonali pravokotni, potem je to gotovo romb.)
Rombu lahko vedno včrtamo krožnico. Stranice romba so tangente te krožnice, zato pravimo, da je romb tangentni štirikotnik.

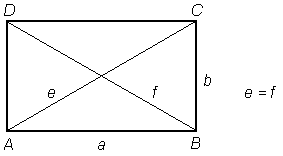
Paralelogram, ki ima vse štiri kote skladne, imenujemo pravokotnik.
Vsak od kotov v pravokotniku meri 90°.
Diagonali pravokotnika sta enako dolgi. (Ta lastnost je v nekem smislu karakteristična: Če sta v nekem paralelogramu diagonali enako dolgi, potem je to gotovo pravokotnik.)
Pravokotniku lahko vedno očrtamo krožnico. Stranice pravokotnika so tetive te krožnice, zato pravimo, da je pravokotnik tetivni štirikotnik.
Vsak od kotov v pravokotniku meri 90°.
Diagonali pravokotnika sta enako dolgi. (Ta lastnost je v nekem smislu karakteristična: Če sta v nekem paralelogramu diagonali enako dolgi, potem je to gotovo pravokotnik.)
Pravokotniku lahko vedno očrtamo krožnico. Stranice pravokotnika so tetive te krožnice, zato pravimo, da je pravokotnik tetivni štirikotnik.
Paralelogram, ki ima vse štiri stranice skladne in vse štiri kote enako velike, imenujemo kvadrat.
Kvadrat ima vse lastnosti romba in pravokotnika.
Kvadrat ima vse lastnosti romba in pravokotnika.
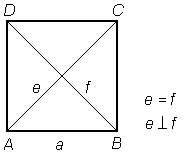
Trapez
Trapez je štirikotnik, ki ima točno en par vzporednih stranic. Ti dve stranici imenujemo osnovnici trapeza (in ju ponavadi označujemo a in c), ostali dve stranici pa sta kraka (b in d).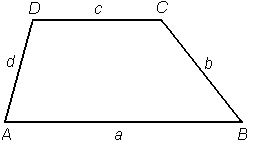
Lastnosti trapeza:
Za kote velja: α + δ = 180°, β + γ = 180°.
Za kote velja: α + δ = 180°, β + γ = 180°.
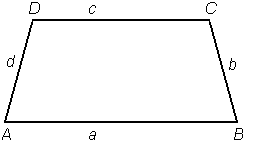
Enakokraki trapez je trapez, ki ima kraka enako dolga (b = d).
V enakokrakem trapezu velja dodatno: α = β, γ = δ.
Diagonali enakokrakega trapeza sta enako dolgi.
Enakokrakemu trapezu lahko vedno očrtamo krožnico. Stranice enakokrakega trapeza so tetive te krožnice, zato pravimo, da je enakokraki trapez tetivni štirikotnik.
V enakokrakem trapezu velja dodatno: α = β, γ = δ.
Diagonali enakokrakega trapeza sta enako dolgi.
Enakokrakemu trapezu lahko vedno očrtamo krožnico. Stranice enakokrakega trapeza so tetive te krožnice, zato pravimo, da je enakokraki trapez tetivni štirikotnik.
Deltoid
Deltiod je štirikotnik, ki ima dva para skladnih sosednjih stranic.Deltoid je vedno simetričen glede na eno od diagonal.
Možna sta dva načina označevanja deltoida, glede na to ali je simetrala diagonala AC ali BD:
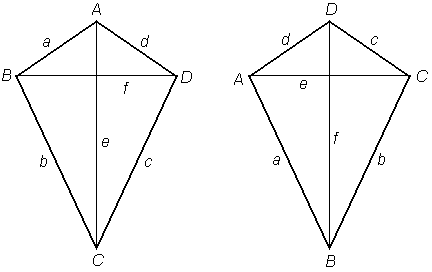
Diagonali deltoida sta pravokotni in tista, ki je simetrala deltoida, drugo diagonalo razpolavlja.
Deltoid je lahko konveksen ali pa tudi konkaven. Konveksnemu deltoidu lahko vedno včrtamo krožnico – tak deltoid je tangentni štirikotnik.
Tangentni štirikotnik
Tangentni štirikotnik je konveksni štirikotnik,
ki mu lahko včrtamo krožnico. Stranice štirikotnika so potem tangente te krožnice.
Karakteristična lastnost tangentnega štirikotnika:
Vsota dolžin nasprotnih stranic je enaka za oba para nasprotnih stranic, torej:
a + c = b + d
Primeri tangentnih štirikotnikov:
Karakteristična lastnost tangentnega štirikotnika:
Vsota dolžin nasprotnih stranic je enaka za oba para nasprotnih stranic, torej:
a + c = b + d
Primeri tangentnih štirikotnikov:
- Vsak romb je tangentni štirikotnik.
- Vsak kvadrat je tangentni štirikotnik.
- Vsak konveksni deltoid je tangentni štirikotnik.

Tetivni štirikotnik
Tetivni štirikotnik je štirikotnik,
ki mu lahko očrtamo krožnico. Stranice štirikotnika so potem tetive te krožnice.
Karakteristična lastnost tetivnega štirikotnika:
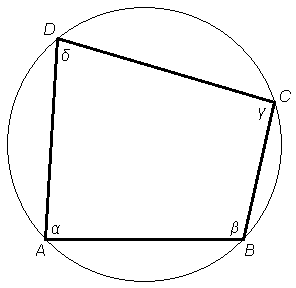
Vsota nasprotnih kotov je enaka za oba para nasprotnih kotov (in znaša 180°), torej:
α + γ = β + δ = 180°
Primeri tetivnih štirikotnikov:
Karakteristična lastnost tetivnega štirikotnika:
Vsota nasprotnih kotov je enaka za oba para nasprotnih kotov (in znaša 180°), torej:
α + γ = β + δ = 180°
Primeri tetivnih štirikotnikov:
- Vsak pravokotnik je tetivni štirikotnik.
- Vsak kvadrat je tetivni štirikotnik.
- Vsak enakokraki trapez je tetivni štirikotnik.
Glej tudi poglavje: Obseg in ploščina
| Kazalo poglavij | Pravokotni trikotnik | Podobnost | Abecedno kazalo |