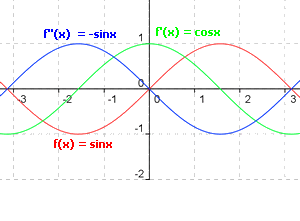Iz doslej znanega vemo, da obstajajo za odvedljive funkcije odvodi, ki so zopet funkcije. Znani primeri za to so elementarne funkcije. Zakaj ne bi odvod še enkrat odvajali?

Naj bo funkcija f odvedljiva na [a,b]. Potem je njen odvod f' nova funkcija f': [a,b] → R. Če je f' v točki x odvedljiva, obstaja njen odvod, ki ga bomo označili z: Vrednosti f''(x) pravimo drugi odvod funkcije f v točki x.
Če se da funkcijo k-krat zaporedoma odvajati, dobimo po k-tih korakih odvajanja k-ti odvod funkcije f, ki ga označimo z f^(k)(x):

f(k)(x) = (f(k-1)(x))'

Višji odvodi za funkcijo f(x) = x⁴ + 5x² + 6

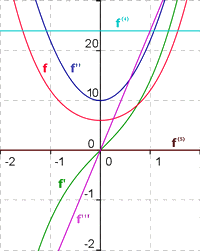Poiščemo najprej njen prvi odvod:

f'(x) = 4·x3 + 5·2·x + 0	=	4·x3 + 10·x

Zdaj odvajamo prvi odvod funkcije f(x), da dobimo njen drugi odvod:

f''(x) = 4·3·x2 + 10

=

12·x2 + 10

Nato odvajamo drugi odvod, da dobim tretji:

f'''(x) = 12·2·x + 0

=

24·x

Odvajamo tretji, da dobimo četrti odvod:

f(4)(x) = 24

Odvajajmo četrti odvod, da dobimo peti:

f(5)(x) = 0

Vsak odvod višji ali enak 5 je 0.

Pomen in uporaba prvega odvoda:

Vrednost prvega odvoda v neki točki predstavlja naklon grafa funkcije v tej točki (tangens kota med tangento in abscisno osjo). Absolutna vrednost odvoda nam pove, kako hitro se funkcija okrog izbrane točke spreminja. Zato rečemo prvemu odvodu tudi hitrost spreminjanja funkcije. Za linearno funkcijo oziroma premice je veljalo, da je ta naraščajoča, če je smerni koeficient ( naklon) pozitiven in padajoča, ko je negativen. Smerni koeficient je nič za vodoravne premice. V odvisnosti od vrednosti prvega odvoda funkcije v neki točki bomo dejali:

• Če je f'(x) > 0, funkcija f v točki x narašča.
• Če je f'(x) < 0, funkcija f v točki x pada.
• Če je f'(x) = 0, funkcija f ima v točki x lokalni ekstrem
  (lokalni minimum, lokalni maksimum, prevoj).

Lokalni minimum je taka točka na grafu (krivulji), iz katere se krivulja v levo in desno dviga. Iz lokalnega maksimuma se krivulja v obe smeri spušča. V prevoju se krivulja zravna, se pa v obeh smereh dviga ali spušča. Lokalne ekstreme moramo tako iskali v ničlah odvoda funkcije. Ničlam odvoda funkcije pravimo tudi stacionarna točke. Opazimo pa lahko, da vsaka ničla odvoda ni nujno ekstremna točka. Poglejmo si funkcijo:

f(x) = x3

Odvajajmo f(x):

f'(x) = 3·x2

f'(0) = 3·02 = 0

Odvod funkcije f(x) v točki 0 je enaka 0 in vendar ta točka ni ekstremna točka.
Za funkcijo f(x) = x³ je v točki 0 prevoj funkcije.

Pomen in uporaba drugega odvoda

Če predstavlja prvi odvod hitrost spreminjanja vrednosti funkcije, predstavlja drugi odvod hitrost spreminjanja hitrosti. Torej ga lahko imenujemo pospešek spreminjanja funkcije.

Nam lahko drugi odvod kakšne vrste je neka stacionarna točka? V lokalnem minimumu se krivulja z leve strani spušča, nato v desno narašča. Odvod je levo od lokalnega minimuma negativen, desno pa pozitiven. Okrog minimuma je odvod naraščajoča funkcija, njegov odvod, ki je drugi odvod dane funkcije, pa je levo in desno pozitiven. Po podobnem sklepanju ugotovimo, da je drugi odvod okrog lokalnega maksimuma negative okrog prevoja pa enak nič. Če velja f'(a)= 0 za neko točko a iz definicijskega območja, potem je glede na vrednost drugega odvoda funkcije f(x) v točki a.

• Če je (pri pogoju f'(a) = 0) f''(a) > 0, je v točki a lokalni minimum funkcije f(x).
• Če je (pri pogoju f'(a) = 0) f''(a) < 0, je v točki a lokalni maksimum funkcije f(x).
• Če je (pri pogoju f'(a) = 0) f''(a) = 0, je v točki a prevoj funkcije f(x).