Št.
Ime točke
Trilinearne koordinate (prva komponenta)
Opomba/Več o tej točki pokukaj na
X1
Incenter
1
X2
Centroid
![]() ALI
ALI ![]() ALI
ALI 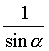
X3
Circumcenter
![]() ALI
ALI ![]()
X4
Orthocenter
![]()
X5
Nine-point center
![]() ALI
ALI ![]()
ALI ![]()
Središče krožnice deveterih točk
X6
Symmedian point, Lemoine point
![]() ALI
ALI ![]()
X7
Gergonne point
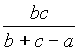 ALI
ALI ![]()
X8
Nagel point
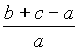 ALI
ALI ![]()
X9
Mittenpunkt
![]() ALI
ALI ![]()
X10
Spiker center
![]()
X11
Feurebach point
![]() ALI
ALI ![]()
ALI ![]()
Dotikališče včrtane in kr. deveterih točk
X13
Fermat point, 1st isogonic p., Torricelli p.
![]() ALI
ALI ![]()
X17
1st Napoleon point
![]()
Prva Napoleonova t.
X18
2st Napoleon point
![]()
X20
De Longchamps point
![]() ALI
ALI
![]()
Presečišče Eulerjeve in Soddyjeve premice
X175
Isoperimetric point
![]()
Središče zunanje Soddyjeve krožnice
X178
Equal detour point
![]()
Središče notranje Soddyjeve krožnice
X181
Appolonius point
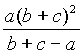 ALI
ALI ![]()
X400
Yff-Malfatti point
![]()
opisana leta 1997